peripatein
- 868
- 0
Hello,
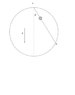
I am asked to show that the time it would take a bead to slide down a smooth cord, positioned at an angle beta wrt the vertical axis, is independent on that angle (between the cord and the
axis). The bead starts its slide from rest.
I was initially not sure whether I should write down force equations or use energy conservation, so I have tried both (should I have used impulse, insead?).
In any case, for the forces acting on the bead sliding down I got:
mgsin(beta) = N ; mgcos(beta) - T = md2x/dt2
And from conservation of energy I got:
mgy = 1/2*mv2
My problem is that I am really not sure any of these equations are flawless as they stand, AND they all seem to be dependent on the angle beta.
Could someone please advise?
Homework Statement
I am asked to show that the time it would take a bead to slide down a smooth cord, positioned at an angle beta wrt the vertical axis, is independent on that angle (between the cord and the
axis). The bead starts its slide from rest.
Homework Equations
The Attempt at a Solution
I was initially not sure whether I should write down force equations or use energy conservation, so I have tried both (should I have used impulse, insead?).
In any case, for the forces acting on the bead sliding down I got:
mgsin(beta) = N ; mgcos(beta) - T = md2x/dt2
And from conservation of energy I got:
mgy = 1/2*mv2
My problem is that I am really not sure any of these equations are flawless as they stand, AND they all seem to be dependent on the angle beta.
Could someone please advise?