Bell's Inequality && polarisation for the layman

[dbertels]

My previous thread on this topic got a bit messy as the gist of the argument was in the middle of the thread and turned out wrong. Hence this new updated version.

One of my favourite articles on Bell's Theorem can be found at
http://www.upscale.utoronto.ca/GeneralInterest/Harrison/BellsTheorem/BellsTheorem.html.

Even though it is geared towards the laymen, I'm having trouble applying the particle spin example to particle polarisation. I would very much appreciate if anyone could check the following reasoning for me:

Assuming the polarisation filters can be set to 3 angles: -30 degrees, 0 degrees, 30 degrees, I have the following states:

A : polarisation of photon after passing a -30 degree filter in the left detector
!A : polarisation of photon after passing a -30 degree filter in the right detector
B : polarisation of photon after passing a 0 degree filter in the left detector
!B : polarisation of photon after passing a 0 degree filter in the right detector
C : polarisation of photon after passing a 30 degree filter in the left detector
!C : polarisation of photon after passing a 30 degree filter in the right detector

I attach a little sketch here that describes the situation.

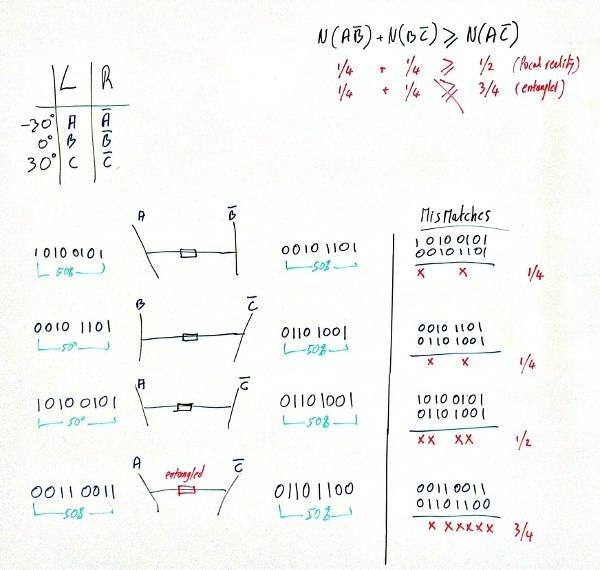
Bell's Inequality states: N(A !B) + N(B !C) >= N(A !C)

Problem I have is that the inequality for polarisation seems to fit for MISMATCHES, i.e for the photons that are NOT matching:

For local reality:
delta 30 degree mismatch + delta 30 degree mismatch >= 2 times delta 30 degree mismatch, or 1/4 + 1/4 >= 1/2
And for entangled photons:
delta 30 degree mismatch + delta 30 degree mismatch >= delta 60 degree mismatch, or 1/4 + 1/4 >= 3/4, which violates Bell's inequality (as it should).

Is this reasoning correct? And if so, why do I need to consider mismatches instead of matches?

 

[zonde]

Is this reasoning correct? And if so, why do I need to consider mismatches instead of matches?

This reasoning is correct.
Photons can be entangled in four different ways:
1. the same polarization when measured at right angles (0,90,180,-90) and the same polarization at diagonal angles (45, -45, 135, -135)
2. the same polarization when measured at right angles (0,90,180,-90) but opposite polarization at diagonal angles (45, -45, 135, -135)
3. opposite polarization when measured at right angles (0,90,180,-90) but the same polarization at diagonal angles (45, -45, 135, -135)
4. opposite polarization when measured at right angles (0,90,180,-90) and opposite polarization at diagonal angles (45, -45, 135, -135)
In your example it is assumed that we use polarization entangled photons of the first type.

 

[DrChinese]

This reasoning is correct.
Photons can be entangled in four different ways:
1. the same polarization when measured at right angles (0,90,180,-90) and the same polarization at diagonal angles (45, -45, 135, -135)
3. opposite polarization when measured at right angles (0,90,180,-90) but the same polarization at diagonal angles (45, -45, 135, -135)

Polarization entangled photons are rotationally invariant. To me, your 1/3 example is conflicting.

For entanglement via parametric down conversion:
There are Type I crystals, which you use 2 of to obtain entanglement where the pair has the same polarization.
There are Type II crystals, which you use 1 of to obtain entanglement where the pair has the opposite polarization.
There are some variations on those types as well, but the above is typical.

 

[zonde]

Polarization entangled photons are rotationally invariant. To me, your 1/3 example is conflicting.

Polarization entangle photons can be rotationally invariant in two different ways:
- when both analyzers are rotated clockwise or counterclockwise
- when one analyzer is rotated clockwise but the other one is rotated counterclockwise and vice versa.
This is the difference between plus or minus sign in description of entangled states $\Psi^\pm$ and $\Phi^\pm$

For entanglement via parametric down conversion:
There are Type I crystals, which you use 2 of to obtain entanglement where the pair has the same polarization.
There are Type II crystals, which you use 1 of to obtain entanglement where the pair has the opposite polarization.
There are some variations on those types as well, but the above is typical.

You can get any of the four states using any source. Look at this paper by Kwiat: New High-Intensity Source of Polarization-Entangled Photon Pairs
There he describes entangled state written in general form:
$\Psi ^\pm = (|HV\rangle +e^{i\alpha} |VH\rangle)/\sqrt2$
Using an additional birefringent phase shifter (or even slightly rotating the down-conversion crystal itself), the value of $\alpha$ can be set as desired, e.g., to the values 0 or $\pi$. (Somewhat surprisingly, a net phase shift of $\pi$ may be obtained by a 90^o rotation of a quarter wave plate in one of the paths.) Similarly, a half wave plate in one path can be used to change horizontal polarization to vertical and vice versa. One can thus very easily produce any of the four EPR-Bell states,
$\Psi ^\pm = (|HV\rangle \pm |VH\rangle)/\sqrt2$
$\Phi ^\pm = (|HH\rangle \pm |VV\rangle)/\sqrt2$

 

[DrChinese]

Polarization entangle photons can be rotationally invariant in two different ways:
- when both analyzers are rotated clockwise or counterclockwise
- when one analyzer is rotated clockwise but the other one is rotated counterclockwise and vice versa.
This is the difference between plus or minus sign in description of entangled states $\Psi^\pm$ and $\Phi^\pm$You can get any of the four states using any source. Look at this paper by Kwiat: New High-Intensity Source of Polarization-Entangled Photon Pairs
There he describes entangled state written in general form:
$\Psi ^\pm = (|HV\rangle +e^{i\alpha} |VH\rangle)/\sqrt2$
Using an additional birefringent phase shifter (or even slightly rotating the down-conversion crystal itself), the value of $\alpha$ can be set as desired, e.g., to the values 0 or $\pi$. (Somewhat surprisingly, a net phase shift of $\pi$ may be obtained by a 90^o rotation of a quarter wave plate in one of the paths.) Similarly, a half wave plate in one path can be used to change horizontal polarization to vertical and vice versa. One can thus very easily produce any of the four EPR-Bell states,
$\Psi ^\pm = (|HV\rangle \pm |VH\rangle)/\sqrt2$
$\Phi ^\pm = (|HH\rangle \pm |VV\rangle)/\sqrt2$

Measurements at 0 and 90 degrees should yield the same matching relationship as measurements at -45 and 45 degrees on an apples to apples basis. I agree that you can also shift the relationship as desired $\alpha$. And there may be tricks you can play that otherwise change the usual dependence on theta.

I think you are saying that in some Bell states: Measurements at 0 and 90 degrees yield the opposite matching relationship as measurements at 45 and -45 degrees respectively. Is that the nuance you are referring to? I am not sure I am following.

 

[zonde]

Measurements at 0 and 90 degrees should yield the same matching relationship as measurements at -45 and 45 degrees on an apples to apples basis. I agree that you can also shift the relationship as desired $\alpha$. And there may be tricks you can play that otherwise change the usual dependence on theta.

You can calculate theta by subtracting two angles or by adding two angles.

I think you are saying that in some Bell states: Measurements at 0 and 90 degrees yield the opposite matching relationship as measurements at 45 and -45 degrees respectively. Is that the nuance you are referring to? I am not sure I am following.

Yes, that's the point.

 

[DrChinese]

Yes, that's the point.

1. So I would conclude that Measurements at 0 and 90 degrees should yield the same matching relationship as measurements at -45 and 45 degrees (in my previous post).

2. I guess I don't follow how -45 and 45 degrees ends up different with a different relationship than 45 and -45 degrees respectively. My poor brain can't picture this. I have seen your reference before, guess I better re-read.

 

[dbertels]

1. the same polarization when measured at right angles (0,90,180,-90) and the same polarization at diagonal angles (45, -45, 135, -135)

In your example it is assumed that we use polarization entangled photons of the first type.

Thanks Zonde, sorry to bring this back to basics (as the current discussion is no doubt more meaningful), but can you please explain how you connect my situation (0, 30, -30) to your first entanglement situation?

 

[Mentz114]

Is this reasoning correct? And if so, why do I need to consider mismatches instead of matches?

The number of matches and mismatches are related N=mismatches + matches.

The correlation which is in [-1,1] is defined as

( matches - mismatches)/( matches+mismatches) = ( matches - mismatches)/N

 

[zonde]

Thanks Zonde, sorry to bring this back to basics (as the current discussion is no doubt more meaningful), but can you please explain how you connect my situation (0, 30, -30) to your first entanglement situation?

Look at formula (10) in this paper: http://arxiv.org/abs/quant-ph/0205171
$P_{VV}(\alpha,\beta)=\frac{1}{2}cos^2(\beta-\alpha)$
This formula describes correlation for my first entanglement type. You can plug in the angles from your example and get the numbers you where using.

 

[dbertels]

Thanks for all your help - that was really useful..