Is the Bernoulli Equation enough to determine pump selection?

[Tom Hardy]

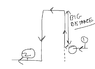
Here is an illustration of something that came into my head:

http://imgur.com/a/V9V8S

(also attached to question)

If we do a energy balance (in terms of head) between point 1 and point 2 (ignoring friction for now, it's not really important):

$$\frac{P_1}{\rho g} + \frac{v^2_1}{2g} + z_1 + h_p = \frac{P_2}{\rho g} + \frac{v^2_2}{2g} + z_2 $$

Assume the pressure is the same so..:

$$ h_p = \bigg( \frac{v^2_2}{2g} - \frac{v^2_1}{2g} \bigg) + (z_2 - z_1)$$

Fine, but this is what I have an issue with, the end result doesn't really take into account the huge distance the liquid has to go up by. When I'm trying to choose a pump, I have to pick an operating head and flow rate. The issue is, the above equation could give me a required pump head that's very small say 5m or something. If the big distance the liquid has to go up is 100m, this 5m head pump won't provide, so how do I pick a pump in this case?

 

[Tom Hardy]

I think I should just do two balances, first one for 1 to the top, and then another balance from the top to the bottom and solve simultaneously

Edit: So if I do a balance between the top and point 3, I can work out the required velocity at the top I need to get for the whatever I want at the bottom, and then I can solve for pump head at point 1.

 

[russ_watters]

I think I should just do two balances, first one for 1 to the top, and then another balance from the top to the bottom and solve simultaneously

You can do that...you might find they combine and simplify via subtraction...

Bernoulli's is a conservation of energy statement. That means you can compare/equate any two points along the flow with it. If you are uncomfortable with how the flow looks at other points, you are welcome to throw them into the analysis as well.

As someone who selects pumps from time to time, I will say that there is a potential hidden issue with elevation changes, as pumps require a certain amount of positive suction head.

 

[Tom Hardy]

You can do that...you might find they combine and simplify via subtraction...

Bernoulli's is a conservation of energy statement. That means you can compare/equate any two points along the flow with it. If you are uncomfortable with how the flow looks at other points, you are welcome to throw them into the analysis as well.

As someone who selects pumps from time to time, I will say that there is a potential hidden issue with elevation changes, as pumps require a certain amount of positive suction head.

Ah, there's the issue. At the end, if I do the subtraction, I'll be left with $$(z_3 - z_2)$$ as my change in height term. This completely ignores the fact the pump has to raise the liquid to $$z_2$$. So when I'm looking at a pump operating curve, I may pick something that's operating at say, 5m of head and this is fine if I didn't have to take the liquid up to a height greater than 5m.

The only way I see to deal with this, is to solve the two separately. First I can can solve for the velocity I need at the top to get the velocity I want at the bottom, then once I have this velocity, I can just get the proper value for required pump head.

 

[russ_watters]

Ah, there's the issue. At the end, if I do the subtraction, I'll be left with $$(z_3 - z_2)$$ as my change in height term. This completely ignores the fact the pump has to raise the liquid to $$z_2$$. So when I'm looking at a pump operating curve, I may pick something that's operating at say, 5m of head and this is fine if I didn't have to take the liquid up to a height greater than 5m.

No, I do think you missed the second step of the logic: the pump only cares about the water flowing into it. It doesn't care where the water has been. So the up and down has no impact on the pump. The fact that the up and down simplifies right out of the equation reflects that reality.

In your case, since you are on the discharge side, you don't have the issue I mentioned with suction head.

 

[Tom Hardy]

No, I do think you missed the second step of the logic: the pump only cares about the water flowing into it. It doesn't care where the water has been. So the up and down has no impact on the pump. The fact that the up and down simplifies right out of the equation reflects that reality.

In your case, since you are on the discharge side, you don't have the issue I mentioned with suction head.

I think you misread my diagram, the water is coming from the left, and it still has to go up and down. It has not gone up and down yet

 

[russ_watters]

I think you misread my diagram, the water is coming from the left, and it still has to go up and down. It has not gone up and down yet

?? I'm not sure what I am missing; the flow arrows definitely appear to be pointing to the left...

 

[Tom Hardy]

?? I'm not sure what I am missing; the flow arrows definitely appear to be pointing to the left...

Right the flow is going to to the left, so it goes up and down after the pump

 

[russ_watters]

Right the flow is going to to the left, so it goes up and down after the pump

Ok, so the pump only cares about the flow and head it sees at the discharge. The specifics of the system further downstream don't matter to it except for how they impact the flow and head (and as you found, the up and down part subtracts itself out).

 

[Tom Hardy]

Ok, so the pump only cares about the flow and head it sees at the discharge. The specifics of the system further downstream don't matter to it except for how they impact the flow and head (and as you found, the up and down part subtracts itself out).

I get that, but the thing is, say the 'big distance' is REALLY big, how will a 5m head pump be able to pump water up 200m? If I got rid of the part where it comes back down, the pump would not work, so why does it magically work when I add the part where it goes down?

 

[Nidum]

(1) Many possible problems with this configuration . Most common are :

Start up problem where the pump may have to build up a head of fluid in the initially empty riser pipe .

Flow separation in the cross over pipe at the top .

(2) There are two distinct cases to analyse for the steady state condition . They are where :

The back pressure at the final outlet is relatively high .

The back pressure at the final outlet is relatively low or atmospheric .

(3) Note that :

Simple Bernoulli flow may not be adequate to analyse this problem completely .

The analysis with a positive displacement pump is different from the analysis with a non positive displacement pump .

 

[Tom Hardy]

(1) Many possible problems with this configuration . Most common are :

Start up problem where the pump may have to build up a head of fluid in the initially empty riser pipe .

Flow separation in the cross over pipe at the top .

(2) There are two distinct cases to analyse for the steady state condition . They are where :

The back pressure at the final outlet is relatively high .

The back pressure at the final outlet is relatively low or atmospheric .

(3) Note that :

Simple Bernoulli flow may not be adequate to analyse this problem completely .

The analysis with a positive displacement pump is different from the analysis with a non positive displacement pump .

It's a centrifugal pump

 

[Nidum]

Too many conditional answers needed to deal with this type of problem in abstract . Draw up a plausible real system for us to look at ?

 

[russ_watters]

I get that, but the thing is, say the 'big distance' is REALLY big, how will a 5m head pump be able to pump water up 200m?

Let's stay at 5m for a sec: the answer is that it doesn't have to. The water flowing up is pulled up by the water flowing down the other side, like a siphon.

If you go higher/lower than 10m though you may run into a problem where the water flowing down the other side pulls a vacuum.

 

[Nidum]

If you go higher/lower than 10m though you may run into a problem where the water flowing down the other side pulls a vacuum.

+1

 

[Tom Hardy]

Too many conditional answers needed to deal with this system in abstract . Draw up a plausible real system for us to look at ?

Let's stay at 5m for a sec: the answer is that it doesn't have to. The water flowing up is pulled up by the water flowing down the other side, like a siphon.

If you go higher/lower than 10m though you may run into a problem where the water flowing down the other side pulls a vacuum.

Ah, I see, so the only issue at the start is priming the system so that a siphon exists?

 

[Nidum]

For very large rise and fall heights it is common practice to separate the down going flow from the up going flow using a big header tank .

Bad second choice solution is to put a restrictor at bottom of down pipe .

 

[Tom Hardy]

For very large rise and fall heights it is common practice to separate the down going flow from the up going flow using a big header tank .

Bad second choice solution is to put a restrictor at bottom of down pipe .

Thanks, it's not really large in reality, it was just the concept I was confused about.

 

[russ_watters]

Ah, I see, so the only issue at the start is priming the system so that a siphon exists?

Yes! If the system is not pre-filled, and is filled with that pump, the pump will have to overcome the entire head of the rise.