Bernoulli Principle For Pitot Tubes

[person123]

Here is the setup:

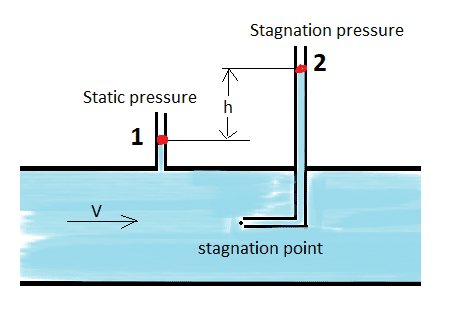
Apply Bernoulli Principle to the top (free surface) of the two pitot tubes (1 for static and 2 for dynamic with the points colored in red): $$\frac{p_1}{\rho_w g}=h+\frac{p_2}{\rho_w g}$$
The difference in air pressure would give the following:$$p_1=p_2+h\rho_{air} g$$
Solving for h would give: $$\frac{p_2+h\rho_{air}g}{\rho_w g}=h+\frac{p_2}{\rho_w g}$$ $$\frac{p_2}{\rho_w g}+h\frac{\rho_{air}}{\rho_w}=h+\frac{p_2}{\rho_w g}$$ $$\frac{\rho_{air}}{\rho_w}=1$$

Which is clearly false. Does anyone know what the error here is?

 

[Lnewqban]

Who is #1 and who is #2 in the posted picture?
Stagnation pressure = static pressure + dynamic pressure

 

[person123]

I clarified the location of the points by coloring them in red.

 

[person123]

I'm assuming the two free surfaces are still and the system has reached a steady state.

 

[russ_watters]

Which is clearly false. Does anyone know what the error here is?

I don't see that you've given us a question that the problem is trying to answer.

The first statement seems to be describing the height of two imaginary columns of water. Why? Why aren't they on the diagram?

 

[person123]

The first statement seems to be describing the height of two imaginary columns of water. Why? Why aren't they on the diagram?

$h$ is referring to the difference in height between the two real columns of water in the pitot tube. $p_1$ and $p_2$ are the pressures at the free surface of these tubes. I'm equating the head between these two points.

I don't see that you've given us a question that the problem is trying to answer.

I'm not giving a question; instead I'm just showing what seems to be a contradiction that's confusing me.

 

[russ_watters]

$h$ is referring to the difference in height between the two real columns of water in the pitot tube. $p_1$ and $p_2$ are the pressures at the free surface of these tubes. I'm equating the head between these two points.

But your terms don't appear to me to be describing that relationship. Your terms are not describing the heights of the water columns on the diagram, they are describing two other, not pictured, water columns that aren't different by $h$. I don't think the mathematical statement is true/describes the diagram.

Edit:

I'm not giving a question; instead I'm just showing what seems to be a contradiction that's confusing me.

I don't think that's sufficient. Why did you do this math? What did you think it would show? The first statement describes...something, but as far as I can tell you didn't say what it is. I think the answer here is that that first statement isn't describing what you think it is describing.

 

[boneh3ad]

EDIT: Sorry, the forum screwed up a bunch of stuff and delete some things seemingly randomly.

Your equations don't appear to be related to Bernoulli from what I can tell. They are just adding hydrostatic pressures. If you want to incorporate Bernoulli, you would have a velocity in there. Either way, make sure you include all heights or you can rapidly lose track of things and get confused.

Let's call $p_1$ the pressure at the port for tube 1, $p_2$ the pressure at the port for the Pitot tube 2, $h$ the difference in height between the two water columns, $h_1$ is the height of the water in column 1, $h_2$ is the height of the water in column 2 from the top of the pipe, and $R$ the pipe radius (i.e. the height difference between the entrance to port 1 and port 2.

Then,
$$p_1=\rho_wgh_1+p_{atm},$$
$$p_2=\rho_w g R + \rho_wgh_2+p_{atm},$$
and
$$p_2 - p_1 = \rho_w g (h_2 + R - h_1) = \rho_w g (R+h).$$

From Bernoulli's equation, we also know (since $v=0$ at the tip of the Pitot)
$$p_1 + \dfrac{1}{2}\rho_w v^2 + \rho_w g R= p_2,$$
or
$$p_2 - p_1 = \dfrac{1}{2}\rho_w v^2 + \rho_w g R.$$
Therefore,
$$\rho_w g h = \dfrac{1}{2}\rho_w v^2,$$
or
$$v = \sqrt{2 g h}.$$

 

[hutchphd]

Where does :

The difference in air pressure would give the following:$$p_1=p_2+h\rho_{air} g$$

Come from??

 

[russ_watters]

Where does :

The difference in air pressure would give the following:$$p_1=p_2+h\rho_{air} g$$

Come from??

That part I do think I get: over small distances the density of the air can be considered constant, so the atmospheric pressures at the two points do have that relationship.

 

[russ_watters]

Your equations don't appear to be related to Bernoulli from what I can tell. They are just adding hydrostatic pressures.

Agreed, the pito/static probes are totally irrelevant to what the OP is doing. The problem can be simplified to show two vertical tubes, closed at the bottom, with different amounts (heights) of water in them.

 

[hutchphd]

I am woefully ignorant here but the pitot tube is measuring some kind of "dynamic" pressure from the flow ...my apologies if my terminology is wrong. Clearly the preceding equation and this one refer to different pressures somehow.edit: I just looked at the picture closely. The flow is in the water! Are these really pitot tubes? I defer to those with actualknowledge!

 

[boneh3ad]

Certainly, and they differ due to the velocity (part of dynamic pressure) and height difference.

 

[russ_watters]

I am woefully ignorant here but the pitot tube is measuring some kind of "dynamic" pressure from the flow ...my apologies if my terminology is wrong. Clearly the preceding equation and this one refer to different pressures somehow.

The pito tube measures total pressure, the static tube static pressure and the difference is velocity/dynamic pressure. But the OP isn't doing any work on that relationship.

The OP is examining the water columns themselves, not the flow situation.

 

[Chestermiller]

Summary:: If you apply Bernoulli Principle between the free surface in two pitot tubes, one measuring static pressure and one measuring stagnation pressure, the answer seems false to me.

Here is the setup:
View attachment 270140
Apply Bernoulli Principle to the top (free surface) of the two pitot tubes (1 for static and 2 for dynamic with the points colored in red): $$\frac{p_1}{\rho_w g}=h+\frac{p_2}{\rho_w g}$$

This first equation of yours is already incorrect. It applies only to a system that is at static equilibrium, and this system is not at static equilibrium. The correct relationship, neglecting the tiny pressure difference due to the different elevations in the air is $$p_1=p_2$$
If H is the elevation of point 1 above the centerline of the tube and $p'_1$ is the pressure at the centerline, then $$p'_1=p_1+\rho gH$$ Then the stagnation pressure at the inlet to the pitot tube is $$p_s=p'_1+\frac{1}{2}\rho v^2=p_1+\rho gH+\frac{1}{2}\rho v^2$$where v is the horizontal flow velocity at point 1'. The pressure $p'_2$ at the end of the horizontal section of the pitot tube directly below point 2 is also equal to the stagnation pressure: $$p'_2=p_s=p_1+\rho gH+\frac{1}{2}\rho v^2$$Starting from point 2, the pressure $p'_2$ is also given by: $$p'_2=p_2+\rho g (h+H)$$ So, combining these last two equations yields: $$p_1+\rho gH+\frac{1}{2}\rho v^2=p_2+\rho g (h+H)$$But, since $p_1=p_2$, as @boneh3ad indicates, this reduces to $$\frac{1}{2}\rho v^2=\rho g h$$