dE_logics
- 742
- 0
In a pipe of varying diameter in which an ideal fluid is flowing, there's an increment in the kinetic energy of each particle as it reaches a region of lower cross section from a higher cross section in the pipe.
Following the law of conservation of energy, there should be an energy transfer in some way which allows this increment in kinetic energy; the energy stored by virtue of pressure in the fluid is said to provide this energy but in an ideal fluid, there can't be any energy stored though pressure...so considering an ideal fluid in this situation, where does this energy come from?
E.g in this case of an ideal fluid flow -
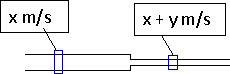
This additional K.E by virtue of y cannot come though conversion of pressure to K.E since an ideal fluid cannot store energy using pressure.
I've tried by best to explain the situation, but if you still do not understand, please complaint.
Following the law of conservation of energy, there should be an energy transfer in some way which allows this increment in kinetic energy; the energy stored by virtue of pressure in the fluid is said to provide this energy but in an ideal fluid, there can't be any energy stored though pressure...so considering an ideal fluid in this situation, where does this energy come from?
E.g in this case of an ideal fluid flow -
This additional K.E by virtue of y cannot come though conversion of pressure to K.E since an ideal fluid cannot store energy using pressure.
I've tried by best to explain the situation, but if you still do not understand, please complaint.
Attachments
Last edited: