- #1
Peach
- 80
- 0
Homework Statement
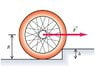
You are trying to raise a bicycle wheel of mass m and radius R up over a curb of height h. To do this, you apply a horizontal force F.
What is the least magnitude of the force F_vec that will succeed in raising the wheel onto the curb when the force is applied at the center of the wheel?
Homework Equations
F = 0
torque_total = 0
The Attempt at a Solution
I've tried for the last hours to figure out how to do this but I'm stuck. I've drawn a free body diagram with the horizontal force and also, the force the curb is exerting on the wheel as well? They must equal right..? I don't really have any idea how to start this problem other than that though. So frusterated sigh. :( Any help is appreciated, thanks.
Pic: http://img85.imageshack.us/img85/9453/yffigure1142xt0.jpg
Attachments
Last edited by a moderator: