- #1
A M
- 83
- 16
Summary: I always confuse Binding Energy with Released Energy in such processes. Which one comes from mass defect?
For example in a Deuterium-Tritium fusion two nuclei with lower binding energy converse to He-4 with much higher binding energy (and a neutron). The released energy is 17.6 MeV.
What exactly happens to mass defect?
Is it conversed to the higher binding energy of ∝-particle
or the released kinetic energy of the products?
Anyone could help me with this problem?
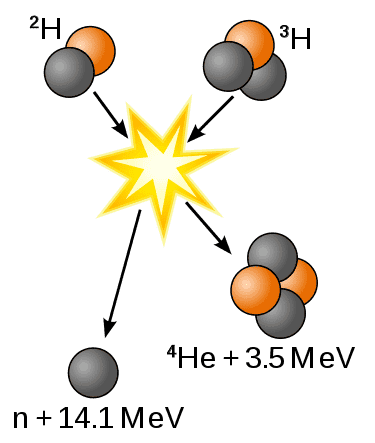 Fusion of deuterium with tritium creating helium-4, freeing a neutron, and releasing 17.59 MeV as kinetic energy of the products while a corresponding amount of mass disappears, in agreement with kinetic E = Δmc2, where Δm is the decrease in the total rest mass of particles....This difference in mass arises due to the difference in atomic "binding energy" between the atomic nuclei before and after the reaction.
Fusion of deuterium with tritium creating helium-4, freeing a neutron, and releasing 17.59 MeV as kinetic energy of the products while a corresponding amount of mass disappears, in agreement with kinetic E = Δmc2, where Δm is the decrease in the total rest mass of particles....This difference in mass arises due to the difference in atomic "binding energy" between the atomic nuclei before and after the reaction.
Isn't it a contrast?!
https://en.wikipedia.org/wiki/Nuclear_fusion
For example in a Deuterium-Tritium fusion two nuclei with lower binding energy converse to He-4 with much higher binding energy (and a neutron). The released energy is 17.6 MeV.
What exactly happens to mass defect?
Is it conversed to the higher binding energy of ∝-particle
or the released kinetic energy of the products?
Anyone could help me with this problem?
Isn't it a contrast?!
https://en.wikipedia.org/wiki/Nuclear_fusion
Last edited: