foxyfresh
- 4
- 0
QUESTION 1:
9. Your first cousin died of Tay-Sachs disease (autosomal recessive, incidence 0.09% (about 1 in 1100)).
You are not affected, nor is anyone else in your extended family. What is the approximate chance that
you are a carrier?
A. 5.8%
B. 12.5%
C. 25%
D. 50%
E. 67%
THE BOOK ASNWER IS C: 25%
I don't really understand why the answer is 25%. So, I try to make a logical explanation for that. I'm not sure if my reasoning is correct; thus, please help me see if my reasoning is correct or not. If it's wrong, please tell me where I went wrong. Thank you :)
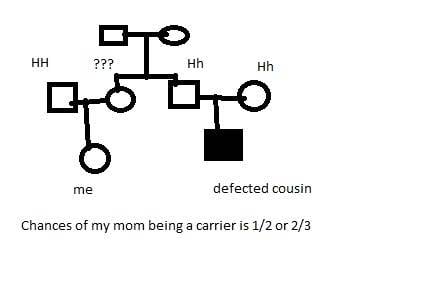
What I did whas that I I drew out my pedegre. Starting from my First cousin family, I know for sure that the Uncle is is a carrier (Aa) and he must have married a wife who is also a carrier (Aa) and that is how they got an affected son. Thus, this leads to the fact that either both of my grandparents are carriers (Aa x Aa) or only one of them is a carrier (Aa x AA). As a result, the chances that my mom (who is related to the uncle who has a defected child) is a carrier is either (2/3 or 1/2) depending if my grandparents genotype, respectively.
Thus, if my mom chances of being a carrier is 1/2 then my chance of being a carrier is 1/4. (given that my dad is not a carrier b/c CF is a rare disease)
However, if my mom chance of being a carrier is 2/3 then my chance of being a carrier is (2/3)x(1/2)=(1/3) As a result, I could either be 1/4 or 1/3. But since the answer only provide the choice of 1/4 and not 1/3. This leave C to be the correct answer.
This is my interpretation of it; however, I'm not sure if this logic reasoning is correct.
Picture of my "assumed" pedegry
 -----
-----
QUESTION 2:
28. The actual carrier frequency of cystic fibrosis in the Caucasian population is about 50% lower than
what the Hardy-Weinberg formula would predict based on the number of affected individuals. A
reasonable explanation for this might be (choose none, one, or more than one):
(A) inbreeding (B) heterozygote superiority (C) carriers may have a mild disease phenotype that is
somewhat disadvantageous (D) genetic drift.
ANSWER IS C
I was wondering if you can check if my logic reasoning for this question is correct.
Well, if you think about it, the carrier are lower in # if their frequency is lower in compare to the Hardy Weinberg prediction.
Since the defected people are dead, leaving only the carrier behind. So, if the carrier is normal, then their number SHOULD resemble that of the Hardy Weinberg prediction, but since the carrier number is small, this indicate that the carrier is also somewhat hurt by having a recessive alleles of CF. (leading to their low in numbers)
Homework Statement
9. Your first cousin died of Tay-Sachs disease (autosomal recessive, incidence 0.09% (about 1 in 1100)).
You are not affected, nor is anyone else in your extended family. What is the approximate chance that
you are a carrier?
A. 5.8%
B. 12.5%
C. 25%
D. 50%
E. 67%
THE BOOK ASNWER IS C: 25%
Homework Equations
I don't really understand why the answer is 25%. So, I try to make a logical explanation for that. I'm not sure if my reasoning is correct; thus, please help me see if my reasoning is correct or not. If it's wrong, please tell me where I went wrong. Thank you :)
The Attempt at a Solution
What I did whas that I I drew out my pedegre. Starting from my First cousin family, I know for sure that the Uncle is is a carrier (Aa) and he must have married a wife who is also a carrier (Aa) and that is how they got an affected son. Thus, this leads to the fact that either both of my grandparents are carriers (Aa x Aa) or only one of them is a carrier (Aa x AA). As a result, the chances that my mom (who is related to the uncle who has a defected child) is a carrier is either (2/3 or 1/2) depending if my grandparents genotype, respectively.
Thus, if my mom chances of being a carrier is 1/2 then my chance of being a carrier is 1/4. (given that my dad is not a carrier b/c CF is a rare disease)
However, if my mom chance of being a carrier is 2/3 then my chance of being a carrier is (2/3)x(1/2)=(1/3) As a result, I could either be 1/4 or 1/3. But since the answer only provide the choice of 1/4 and not 1/3. This leave C to be the correct answer.
This is my interpretation of it; however, I'm not sure if this logic reasoning is correct.
Picture of my "assumed" pedegry
QUESTION 2:
Homework Statement
28. The actual carrier frequency of cystic fibrosis in the Caucasian population is about 50% lower than
what the Hardy-Weinberg formula would predict based on the number of affected individuals. A
reasonable explanation for this might be (choose none, one, or more than one):
(A) inbreeding (B) heterozygote superiority (C) carriers may have a mild disease phenotype that is
somewhat disadvantageous (D) genetic drift.
ANSWER IS C
Homework Equations
I was wondering if you can check if my logic reasoning for this question is correct.
The Attempt at a Solution
Well, if you think about it, the carrier are lower in # if their frequency is lower in compare to the Hardy Weinberg prediction.
Since the defected people are dead, leaving only the carrier behind. So, if the carrier is normal, then their number SHOULD resemble that of the Hardy Weinberg prediction, but since the carrier number is small, this indicate that the carrier is also somewhat hurt by having a recessive alleles of CF. (leading to their low in numbers)
Last edited: