Biot Savart, Electrons, and Cirucular Currents

[cwatki14]

A circular wire ring of diameter 18 cm carries a current of 5.0 A directed as indicated in Figure P.51. A moving electron just happens to be passing through the neighborhood. When the electron is at the center of the circular ring and moving at speed 2.50 multiplied by 106 m/s in the direction indicated in the sketch, find the acceleration of the electron.

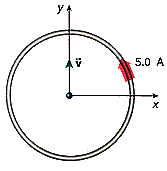
Equations I found relevant:
The Biot Savart Law:
B=(\mu/4\pi)(I)(\intdl x r / r^2)

F=qv x B

Biot Savart solves for the magnetic field, they I can plug this into the force equation, and once I know the force, I can divide by the mass to get the particles acceleration.
I had some issues with the Biot Savart...

I used the following numbers
B=(\mu/4\pi)(5A)(circumference of the circle/r^2)
dl= circumference of the circle which eqauls d\pi. or .5654
since r is the distance from the circle to the particle, it equal the circle's radius which is .9m.
Therefore B=3.4906e-5
I substitute this into the force equation giving me
F=qv x B
The v vector and B vector are perpendicular, so it is just scalar multiplication.
I get F=1.3980e-17
I can then divide this by the mass to get the acceleration.
Thus a= 1.5347e13
I used q= 1.602e-19 and m= 9.1093e-31

All of this led me to a wrong answer...

 

[Gear300]

You got the method right, but the metric units are a bit off: the radius is .09m.

 

[cwatki14]

You got the method right, but the metric units are a bit off: the radius is .09m.

that was a typo. my final answer used .09 as the radius, and I still got the problem wrong.

 

[Gear300]

I still haven't checked the calculations yet...but for the moment, maybe what is needed is a negative (electrons have a negative charge, so the acceleration vector is in the opposite direction when compared to positively charged particles, such as protons).