tryingtolearn1
- 58
- 5
- Homework Statement
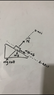
- A block starts at rest and slides down a frictionless plane inclined at an angle $\theta$. What should $\theta$ be so that the block travels a given horizontal distance in the minimum amount of time?
- Relevant Equations
- $$F=ma$$
When drawing a diagram of the forces acting on the block, I have the following forces: $$\sum F_x =mg\sin\theta = ma$$ $$g\sin\theta = a$$ however the solution has $$F_x = ax = (g \sin\theta) \cos \theta$$ but I am not sure how they got that? I know the normal force is $$N=mg\cos\theta$$ but the normal acts on the y-axis.