FancyNut
- 113
- 0
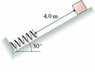
A 26.0 kg box slides 4.0 m down the frictionless ramp shown in the figure, then collides with a spring whose spring constant is 170 N/m.
1-- What is the maximum compression of the spring?
2-- At what compression of the spring does the box have its maximum velocity?
this is killing me...
so acceleration is g sin (theta) which is - 4.9 \frac {m}{s^2} and after using kinematics I figure out the velocity that the block is hitting the spring with which is 6.26 \frac {m}{s} but then what?
If I had a gun to my head and had to write something it'd be this:
\sum F = - m g sin (theta) + k x
x here is delta x.
1-- What is the maximum compression of the spring?
2-- At what compression of the spring does the box have its maximum velocity?
this is killing me...
so acceleration is g sin (theta) which is - 4.9 \frac {m}{s^2} and after using kinematics I figure out the velocity that the block is hitting the spring with which is 6.26 \frac {m}{s} but then what?
If I had a gun to my head and had to write something it'd be this:
\sum F = - m g sin (theta) + k x
x here is delta x.