Blocks attached with spring is released from rest

[lavankohsa]

1. Consider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the pulley, find the maximum elongation of the spring.

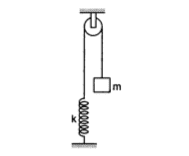
https://drive.google.com/file/d/0B3FvaDRwJ2neQWtBU3JrazVTeEU/view?usp=sharing

Homework Equations

The Attempt at a Solution

I know that i can solve this problem by energy conservation.
mgx=1/2*k*x^2
so x=2mg/k

But i was thinking why can't we solve this problem by balancing of force.
mg=kx
so x=mg/k

because spring will stretched untll mg=kx

Please tell me where i am wrong in this[/B]

 

[gneill]

mg = kx locates the equilibrium point if the system were to come to rest. However, released from a height where the system is not at equilibrium, as the mass falls the system gains kinetic energy from the change in gravitational potential energy. It will shoot by the equilibrium point. In fact the system will continue to oscillate around the equilibrium point so long as there are no energy losses.

 

[lavankohsa]

ok i got it now. it will shoot by the equilibrium point. that's why balancing of force was giving less elongation. so should i do these type of problem by energy conservation and not by balancing of force.

 

[Nathanael]

ok i got it now. it will shoot by the equilibrium point. that's why balancing of force was giving less elongation. so should i do these type of problem by energy conservation and not by balancing of force.

When it's at it's equilibrium, there is no acceleration (which is what you solved for) but when it is at it's maximum elongation, the block is accelerating upwards (so the spring force is greater than mg). That's why using energy would be the way to go.