Body thrown at angle to the horizon taking into account air resistance

[tawki]

Hi every body!
I'm a new guy here, and want to applologize for my Not perfect English.
From the name of the topic you can understand what 'm trying to do here.
ok here is an exercise:
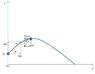
We have tennis ball m=57gr. and diameter of the ball D=6.7sm.
from the start point coordinates X_o=0 & Y_o=0.3m, the ball running speed is V_o=20m/s, with an angle \alpha=15^o. also aking into an account that g=9.8m/s².
Neseccary describe the graph of the ball's flight, with and without air resistance.
i'm trying to use an Microsoft EXCEL for it.
First I want to calculated and build the first graph of the ball without air resistance.
At the beginning let's define projection of starting speed V_ox and V_oy: V_ox=X_o+V_o*cos\alpha and V_oy=Y_o+V_o*sin\alpha.
next we can define total time T_tot=2*V_o*sin\alpha/g.
now we can define the coordinates of the ball at exact time:
X=X_o+V_o*cos\alpha*t
Y=Y_o+V_o*sin\alpha*t-gt²/2
where: t - exact time during ball flight 0≤t≤T_tot
Based on these results, we can now describe the graph.
We can also determine velocity projections on the X and Y axis, as well as the overall speed at each time point:
V_x=V_ox - as the speed of the X-axis does not change with time
V_y=V_oy-g*t
V_total=√(V_ox²+V_oy²).

We now move to the question of the motion of the body with the resistance of the air, and where I have had disagreements.
Let's define the total resistance of the air:
F_tot=c*ρ*V_o²*S/2
where: c - coefficient of resistance of the ball (=0.4); ρ - density of air (=1.2kg/m³); S - sectional area of ​​the ball.
Next we define the projection of force of air resistance on the ball at a time:
F_x=F_tot*cosβ & F_y=F_tot*sinβ
And now finally made the equation of the ball with the air resistance:
X=X_o+V_ox*t-(F_x*t²)/2*m
Y=Y_o+V_oy*t-(g+F_y)*t²/2*m
where: m - coefficient of dynamic viscosity of air.
my ferst question "how to define angle β?", because i did like that: β=arccos(V_x/V_total).
at the end i can not describe the graph of the ball's flight, with and without air resistance.
I really need an advice, of what, where and how i missed something.
Sorry for my inglish (not my native language).

 

[Simon Bridge]

Welcome to PF;
I'd expect air resistance to depend on the square of the instantaneous speed and point opposite to the direction of the instantaneous velocity and not just the value at t=0.

$$\vec{R}_{air}=-\frac{1}{2}c \rho S v\vec{v}$$

You are neglecting the effect of the spin of the ball?

You'll have noticed that the components of the force depend on both components of the velocity.
However - you'll see that your angle beta is a function of time, given by $\beta(t) = \tan^{-1}\big(v_y(t)/v_x(t)\big)$

Solving for air resistance is not simple. You basically have to use a numerical method:
http://wps.aw.com/wps/media/objects/877/898586/topics/topic01.pdf