shogun000
- 11
- 0
Homework Statement
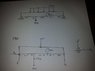
I'm trying to find the boundary conditions for the beam shown in the figure.
Homework Equations
Notation:
V= Shear force
M= Bending moment
The Attempt at a Solution
at x=0 V=R1, M=0
at x=9 V=R3, M=0
In the solution provided at x=9 V=-R2. I don't understand why it's negative, since I took upwards as positive.
Help appreciated!