kosovo dave
Gold Member
- 34
- 0
Homework Statement
I'm trying to find the boundary conditions for the following problem:
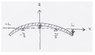
A plate with length 2L is placed on supports at x = L/2 and x = - L/2. The plate is deforming elastically under its own weight (maximum displacement bowing up at x = 0). Both ends of the plate are free boundaries.
The goal is to eventually solve the equation DW'''' = q(x) for the right half of the plate (x > 0).
Homework Equations
D is the flexural rigidity $$\frac{Eh^3}{12(1-\nu^2)}$$
E is Young's Modulus, ν is Poisson's ratio, h is the thickness of the plate, and q = -ρgh.
The Attempt at a Solution
Since the right end of the plate is free, I think the two boundary conditions there are DW''' = 0 (shear force) at x = L and DW'' = 0 (bending moment) at x = L. What are the quantities I should be considering for the boundary conditions at x = 0? I feel like one of them is bending stress.
Last edited: