Calc Magnitude & Direction of A+B+C Vectors

[bumblebeeliz]

Homework Statement

Three vectors, A, B, and C each have a magnitude of 74 units. Their directions relative to the positive direction of the x-axis are 15, 115, & 215 degrees, respectively. Calculate the magnitude and direction of the vectors

a. A+B+C
b. A+B-C
c. C-2A

Homework Equations

R = (square root) R_x² + R_y²

The Attempt at a Solution

So I started with a. :

Ax = (74u) (cos15) = 71.478
Ay = (74u) (sin15) = 19.152

Bx = (-74u) (cos110) = 25.309
By = (74u) (sin110) = 69.537

Cx = (-74u) (cos225) = 52.325
Cy = (-74u) (sin225) = 52.325

Ax+Bx+Cx = 149.112
Ay+By+Cy = 141.014

R = (square root) (149)²+ (141)²
R = 205 units

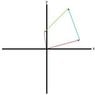
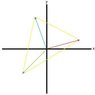
Which doesn't make much sense looking at the first graph? So I attached a second graph because I am not sure which one to use.
Any genius suggestions ?

ps. Red = A Blue = B Green = C Yellow = connected points

 

[Chi Meson]

You stuck negatives in front of the magnitudes for vectors B and C. Why?

The x and y components for B should be - and + respectively. Both components for C should be negative. You allow the sin and cos functions of the absolute angle to determine the pos and neg of the components.

 

[bumblebeeliz]

Thanks for the reply.
I added minuses because I placed the vectors wrongly on the graph. I guess my 2nd graph was correct then.

2nd try:

Ax = (74u) (cos15) = 71.478
Ay = (74u) (sin15) = 19.152

Bx = (74u) (cos110) = -25.309
By = (74u) (sin110) = 69.537

Cx = (74u) (cos225) = -52.325
Cy = (74u) (sin225) = -52.325

Ax+Bx+Cx = -6.156
Ay+By+Cy = 36.364

R = (square root) (-6.156)²+ (36.364)²
R = 36.88 units or 37 units

------

How would I go forth with b. ?

A + B - C

Do I simply do the following:

Ax+Bx - Cx = 98.494
Ay+By - Cy = 141.014

R = (square root) (98.494)²+ (141.014)²
R = 172 units

 

[Chi Meson]

This is apparently correct (I didn't recalculate your numbers, but they appear to be about right). Subtracting a vector is the same thing as adding a vector, except the arrow points in the opposite direction, so all components will switch signs.

Don't forget to find the angle of direction for the resultant. I always take the arctan of (y/x) which will always be the angle from the nearest x-axis. You then have to visually determine which quadrant it lies in, and adjust accordingly for absolute angles.

 

[bumblebeeliz]

I almost forgot to calculate the angles. Thanks a lot!