Calculate Balance Point Distance: A, B, C & D

  • Thread starter Thread starter r4v3n
  • Start date Start date
  • Tags Tags
    Balance Point
AI Thread Summary
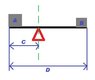
To calculate the balance point on a seesaw-type beam, the distances from the pivot to the center of mass of each weight must be known. The relationship A * E = B * F holds true for a balanced beam, where A and B are the weights and E and F are their respective distances from the pivot. The user is specifically trying to determine the position of 'C' for proper handle placement to ensure balance when lifted. Accurate measurements of the weights' positions relative to the pivot are crucial for this calculation. Understanding these principles will help achieve the desired balance in the product design.
r4v3n
Messages
2
Reaction score
0
Hi All

Ive been racking my brains and i just can't remember how to calculate a 'seesaw' type balance point!?

Please see the attachment - It am trying to work out what 'C' is (I know A, B & D)

Thanks very much
 

Attachments

  • unknown bal point.jpg
    unknown bal point.jpg
    6.4 KB · Views: 557
Physics news on Phys.org
You need to know the distances from below the centre of mass of each of the weights on the beam to the pivot point.

Call these E (on the left) and F (on the right).

Then A * E = B * F if the beam is balanced and weightless.
 
sorry i mean this

Hi

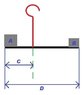
Sorry for the confusion - please see my new attachment with a more accurate diagram.

Basically i am trying to position a handle in the center of a product so when it is lifted it will be balanced.

Again I am after 'C'

thanks very much
 

Attachments

  • unknown bal point2.jpg
    unknown bal point2.jpg
    6.6 KB · Views: 490
No, you have to know where the weights act on the beam.

This is below the center of mass of each weight and not at the end of the beam.
 

Thread 'Why can't Solar panels be hemispherical, or a curved strip type?'

comparing a flat solar panel of area 2π r² and a hemisphere of the same area, the hemispherical solar panel would only occupy the area π r² of while the flat panel would occupy an entire 2π r² of land. wouldn't the hemispherical version have the same area of panel exposed to the sun, occupy less land space and can therefore increase the number of panels one land can have fitted? this would increase the power output proportionally as well. when I searched it up I wasn't satisfied with...
View full post »

Similar threads

Using matrices to balance chemical equations
Replies
11
Views
2K
B Distance between two points on Earth doesn't increase with altitude?
Replies
18
Views
4K
Stress on a spaghetti rod balanced from its middle
Replies
6
Views
1K
Forces applied to a spring-loaded gas pedal
Replies
7
Views
1K
Chemistry How do we interpret the steps in the algorithm to balance a redox equation?
Replies
7
Views
2K
B Simple Counter-balance/Counter-weight Calculation Problem
Replies
3
Views
6K
Calculating distance to balance see-saw
Replies
26
Views
6K
Wheatstone bridge and conditions for current to flow between 2 points
Replies
8
Views
3K
B A tilted container with water inside - how to calculate the distance A?
Replies
11
Views
2K
B Lever balancing physics (video game design)
Replies
18
Views
2K

Hot Threads

Recent Insights

Back
Top