hladon
- 1
- 0
I am writing program which displays car movement through recorded track(2D scene).
So I have a set of points (x1, y1), (x2, y2), (x3, y3), ...(xk, yk), from which track consits.
And I need to calculate an angle between car movement vector and OX(or OY) axis so I could then rotate car image on correct angle.
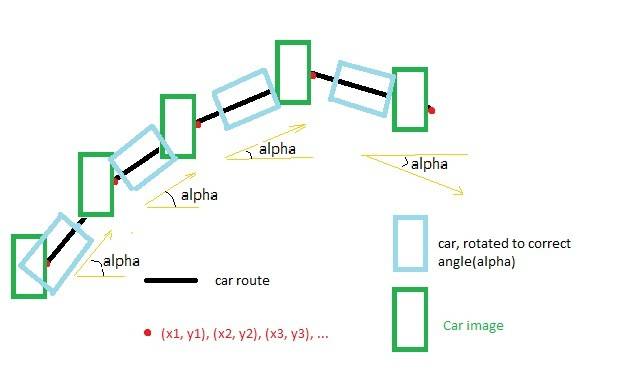 I tried to solve this problem by calculating angle as follows:
I tried to solve this problem by calculating angle as follows:
alpha = arccos( Yk / sqrt( x^2 + Yk^2 ) );
But looks like it's not the perfect solution, because if there is too much points on the route then car image starts dancing through the route:)
I also tried to compute angle between surely different points but the quantity of route points on the square inch can be changed dynamically in my program so if there's too much points, car is rotated really awful :(
Any ideas?
Thanks in advance,
Alex
So I have a set of points (x1, y1), (x2, y2), (x3, y3), ...(xk, yk), from which track consits.
And I need to calculate an angle between car movement vector and OX(or OY) axis so I could then rotate car image on correct angle.
alpha = arccos( Yk / sqrt( x^2 + Yk^2 ) );
But looks like it's not the perfect solution, because if there is too much points on the route then car image starts dancing through the route:)
I also tried to compute angle between surely different points but the quantity of route points on the square inch can be changed dynamically in my program so if there's too much points, car is rotated really awful :(
Any ideas?
Thanks in advance,
Alex
Last edited: