Calculate Center of Mass for a Figure of Uniform Density

In summary, the conversation discusses finding the center of mass of a figure of uniform density. The original poster has divided the figure into four rectangles and obtained individual center of masses, but is unsure if their answer is correct. They are asked for more details, such as the center of mass of each rectangle and the mass of each piece. The conversation then discusses how to find the center of mass using the formula X = m1 x1 + m2 x2 + ... / m1 + m2 ... and how to choose a convenient axis for measurement. Ultimately, the solution is to find the center of mass of each rectangle and then use the formula to find the overall center of mass of the figure.
  • #1
draotic
52
0

Homework Statement


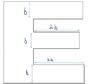
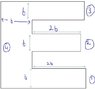
Find the center of mass of figure , of uniform density


Homework Equations


X = m1 x1 + m2 x2 + ... / m1 + m2 ...


The Attempt at a Solution


i broke the figure in 4 rectangles and got individual center of masses
my answers comes out to be
(13b/8 , 5b/2)...
someone told me that's not correct , can someone guide me please ?
 

Attachments

  • final.JPG
    final.JPG
    12.5 KB · Views: 384
Physics news on Phys.org
  • #2
More details are required.
 
  • #3
Show how you got your answer. What did you get for the center of mass of each rectangle? What is the mass of each?
 
  • #4
grzz said:
More details are required.
thats what is given
 
  • #5
Doc Al said:
Show how you got your answer. What did you get for the center of mass of each rectangle? What is the mass of each?

i got 4 coordinates as
1) 2b , b/2
2) 2b , 2.5b
3) 2b , 4.5b
4) 0.5b , 2.5b
 
  • #6
draotic said:
i got 4 coordinates as
1) 2b , b/2
2) 2b , 2.5b
3) 2b , 4.5b
4) 0.5b , 2.5b
Which is which?

And what's the height and width of this object?
 
  • #7
Doc Al said:
Which is which?

And what's the height and width of this object?
here are the measurements
 

Attachments

  • pic.JPG
    pic.JPG
    16.6 KB · Views: 416
  • #8
total height of object is 5b
 
  • #9
OK, looks good. So what did you use for the mass of each piece?
 
  • #10
Doc Al said:
OK, looks good. So what did you use for the mass of each piece?

thats where i am going wrong...
dont know how to proceed , grateful if you could take it from here
 
  • #11
draotic said:
thats where i am going wrong...
dont know how to proceed , grateful if you could take it from here
I'll start you off. Since it's uniform, the mass is proportional to the area. We don't care about the actual mass, only the relative mass of each piece.

What's the area of each piece? Let that represent the mass of each piece.

For example, piece #1 has an area of 2b*b = 2b2.
 
  • #12
all right , 3 pieces have area 2b^2 and the larger one has 5b^2
what now?
 
  • #13
draotic said:
all right , 3 pieces have area 2b^2 and the larger one has 5b^2
what now?
Now start cranking out the center of mass using the formula.
 
  • #14
Doc Al said:
Now start cranking out the center of mass using the formula.

could you please do it for 1 rectangle , i'll do rest
 
  • #15
A trick here is to start your coordinate axis off at the bottom left corner of each rectangle. (Or other corner, just make sure it is all consistent.) What you will find is that each of the smaller rectangles will all have the same center of mass. You could then find the center of mass of the bigger one. Be careful though, they are all (referring to the 3 little ones) only the same in their own respective axes. You would then need to find their coordinates on a different more convenient axis. (Such as the lower left hand corner of the entire E.) From there you can find the center of mass of the entire object.

Sounds kinda tricky but it isn't so bad. This is how I just did it, there are definitely other ways.
 
  • #16
The OP has already figured out the center of mass of each rectangle measured from the same point. All that's left to do is to apply the formula that was posted in the very first post.
 
  • #17
Oh sorry ha! Kind of got a head of my self there. Probably should have read through the post more thoroughly. :p
 

Related to Calculate Center of Mass for a Figure of Uniform Density

What is the center of mass for a figure of uniform density?

The center of mass for a figure of uniform density is the point at which the mass of the figure is evenly distributed in all directions. It is also known as the center of gravity.

How is the center of mass calculated for a figure of uniform density?

The center of mass is calculated by finding the weighted average of the positions of all the individual particles that make up the figure. This is done by multiplying the position of each particle by its mass and then dividing the sum of these values by the total mass of the figure.

Why is it important to calculate the center of mass for a figure of uniform density?

The center of mass is important because it helps us understand the stability and motion of the figure. It also allows us to determine the point where external forces can be applied to the figure without causing it to rotate.

Can the center of mass be located outside of the figure?

Yes, the center of mass can be located outside of the figure. This typically occurs when the figure is irregularly shaped or has holes in it. However, the center of mass will always lie within the boundaries of the figure.

How does the shape of a figure affect its center of mass?

The shape of a figure affects its center of mass by changing the location of the weighted average. Figures with a larger distribution of mass towards one side will have a center of mass closer to that side. Similarly, a figure with a symmetrical shape will have its center of mass at the geometric center.

Similar threads

Finding the center of mass of a homogeneous object
    • Introductory Physics Homework Help
Replies
6
Views
3K
Calculating the center of mass as an astronaut moves on a shuttle
    • Introductory Physics Homework Help
Replies
5
Views
1K
Confusion on product rule for mass of differential volume element
    • Introductory Physics Homework Help
Replies
4
Views
608
Finding Ctr of Mass of object w/ given uniform mass density
    • Introductory Physics Homework Help
Replies
8
Views
1K
Understanding Acceleration and Center of Mass in Shock Absorption
    • Introductory Physics Homework Help
Replies
5
Views
1K
Center of Mass (Subtraction over addition)
    • Introductory Physics Homework Help
Replies
7
Views
2K
Force in Center of Mass frame equaling zero
    • Introductory Physics Homework Help
Replies
7
Views
2K
Solve Pulley-Mass System: m1=4.00 kg, m2=1.00 kg
    • Introductory Physics Homework Help
Replies
2
Views
941
Help Me Solve My Diagram Problem: Calculating Center of Mass
    • Introductory Physics Homework Help
Replies
8
Views
1K
Calculate the density at the centre of the Sun
    • Introductory Physics Homework Help
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top