Calculate Currents Through Ideal Batteries with Kirchhoff's Loop Rule

[subzero0137]

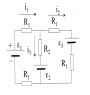
"Use Kirchhoff’s rules to calculate the current through each ideal battery in the figure
below. R1=1Ω, R2=2Ω, ε1=2V, ε2=ε3=4V. You should apply Kirchoff’s loop rule to the ε1-R1-R2-ε2-R1 loop, and the ε2-R2-R1-ε3-R1 loops respectively, each time starting from the negative end of the battery and assuming that the currents flow in the directions shown."



My attempt: i1=i2+i3 (using junction rule).
Left loop:
ε1-i1R1-i3R2-ε2-i1R1=0, therefore i1+i3=-1A.
Right loop:
ε2+i3R2-i2R1-ε3-i2R1=0, therefore i3=i2.

Therefore i1=-2/3A, i2=-1/3A, and i3=-1/3A. But I'm not sure if these are the final values. The question is asking for currents through each ideal battery, so do I have to change the signs of the i2 and i3?

 

[CWatters]

It says "assuming that the currents flow in the directions shown" so I would treat those directions as positive which is what you appear to have done. eg no changes needed. If that turns out to be wrong then I would argue the question is badly worded.

 

[subzero0137]

It says "assuming that the currents flow in the directions shown" so I would treat those directions as positive which is what you appear to have done. eg no changes needed. If that turns out to be wrong then I would argue the question is badly worded.

I see. So the currents in the batteries would flow in the same directions as the currents i1, i2 and i3?

 

[NascentOxygen]

I see. So the currents in the batteries would flow in the same directions as the currents i1, i2 and i3?

Yes, a branch current direction and magnitude is common to all series elements in that branch.

 

[SammyS]

...

Therefore, i1=-2/3A, i2=-1/3A, and i3=-1/3A. But I'm not sure if these are the final values. The question is asking for currents through each ideal battery, so do I have to change the signs of the i2 and i3?

I see. So the currents in the batteries would flow in the same directions as the currents i1, i2 and i3?

You assumed the directions indicated in the figure.

When you assume a direction, you can't always be sure that the current will actually flow in this direction. If the current turns out to be negative, then it flows opposite the direction assumed.

That's the case here for ALL of the currents. That doesn't mean that there's anything wrong with the way the problem is set-up. It simply shows that for the particular values used, the currents flow opposite the assumed direction. This happens frequently when applying Kirchhhoff's circuit rules.

 

[CWatters]

I see. So the currents in the batteries would flow in the same directions as the currents i1, i2 and i3?

Yes, you couldn't have the current through ε1 going the opposite way to current i1.

However the current in the battery is not necessarily in the direction of the arrows on the drawing. That's where the calculated sign comes in. The arrow for I1 defines +ve to be out of the +ve terminal of the battery ε1. However you calculated I1 to be -2/3A which means current is actually flowing into the battery ε1 (eg it's being charged).