zaper
- 49
- 0
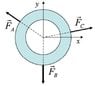
Three forces are applied to a ring (as shown in the photo) that lies on a frictionless surface in the xy plane. The ring has a mass of 100 kg. Fa=200N, Fc=240N and the angle between Fa and Fb is 135°.
What is Fb if:
The system is stationary?
The system accelerates at .5 m/s2?
For some reason I just can't get a grasp on this problem. I understand that to be stationary all forces must cancel out, but I can't figure out how with Fc having a stronger pull in the x direction than Fa how Fb (which appears to go straight down) can stop Fc.
What is Fb if:
The system is stationary?
The system accelerates at .5 m/s2?
For some reason I just can't get a grasp on this problem. I understand that to be stationary all forces must cancel out, but I can't figure out how with Fc having a stronger pull in the x direction than Fa how Fb (which appears to go straight down) can stop Fc.
Attachments
Last edited: