Calculate polarization energy over a set of cuboids

[Glxblt76]

Dear Physics Forums members,

I have a research problem that involves electrostatics. My education is as a chemist, and thus I struggle to accurately represent my problem, so I thought that you guys could help me (and would be interested in the exercise).

Here is an image to summarize my problem.

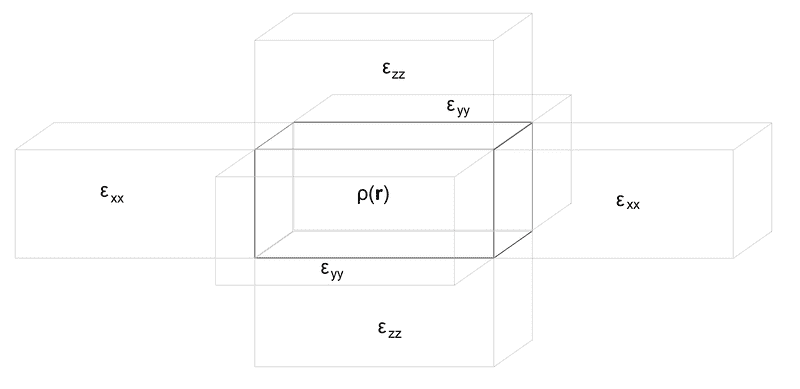
So, in the starting point of my problem, I have my space divided into orthogonal cuboids. The cuboid at the center is particular: there is a charge distribution within it, ρ(r) and its dielectric constant is that of vacuum. All other orthogonal cuboids contain homogeneous, but not isotropic, continua. In the x direction, the dielectric constant is ε_xx, the component of the dielectric constant tensor ε, in y direction it is ε_yy, and in z direction it is ε_zz.
I explicitely represent three cuboids around the central cuboid in each direction, for a total of 7³ - 1 = 342 cuboids. This big cuboid is immersed into a continuum that corresponds to the average value of the dielectric constant tensor ε.

What I would like to write is the equation for the polarization energy of this system (i. e. the energy change caused by replacing a conventional cuboid by a cuboid containing the charge distribution ρ(r) and with the dielectric constant of vacuum).
The system is electrostatic, i e there is no variation of the magnetic field with time. It obeys the two equations:
∇E = ρ/ε₀
∇×E = 0

I know the dimension of the cuboid (the 3 lengths a, b and c from which the cuboid can be reconstructed).

I'm a bit lost and I don't know where to start.
Do some people have suggestions?

All the best!

 

[Glxblt76]

Do not hesitate to ask questions if this does not sound clear to you!

 

[DrDu]

I fear the problem is only solvable numerically. There are very few systems for which it is possible to obtain analytical solutions of the resulting polarisation.

 

[Glxblt76]

I know it, but my question is about how can I do it efficiently, because depending on the method you choose, your solution may be reached slower or faster to the point it's practically indistinguishable from an analytical solution.

 

[DrDu]

I suppose finite element methods are most adequate.

 

[Glxblt76]

Thanks. I will think about it.