Calculate Ratio of Masses A & B After Collision

[Gloyn]

Homework Statement

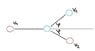
Mass A is moving towards mass B, which is stationary. Collision is elastic. After the collision both masses are mobing symmetrically to the initial direction of motion of mass A.
What is the ratio of masses A and B if the angle between directions of motion of the masses is β?

Homework Equations

Principle of conservation of momentum:
-along the initial direction of A

m_1v_1=m_1u_1cosβ+m_2u_2cosβ

-along the direction perpendicular to the one mentioned above

m_1u_1sinβ=m_2u_2sinβ

Principle of conservationj of energy:

m_1v_1^2=m_1u_1^2+m_2u_2^2

The Attempt at a Solution

Does the 'symmetrical motion' mean that u_1=u_2? If so, then m1=m2, but the answer for this question is m1/m2=2.

 

[mishek]

Hello, I think that they are moving like I sketched. You said mobing symmetrically to the initial direction of motion.

 

[TSny]

Hello, Gloyn.

I interpret the wording as saying that β is the angle between the u₁ and u₂ directions. Also, I interpret "moving symmetrically to the initial direction of A" as meaning that u₁ and u₂ make the same angle with respect to the initial direction of motion of A.

As you say, if you also require u₁ = u₂ then the ratio of masses would have to be 1. So, I would assume that u₁ ≠ u₂. But then, I would think that the answer for the ratio of the masses would depend on β. Did they specify a value of β?

 

[Gloyn]

Yes, they did. So they're not in symmetricall positions in every moment, but paths are symmetrical, right? What can we do about it then? Those three equations i mentioned are not enough, i guess?

 

[TSny]

Yes, they did.

Are you saying they did specify a value for β? If so, what value was given?

So they're not in symmetrical positions in every moment, but paths are symmetrical, right? What can we do about it then? Those three equations i mentioned are not enough, i guess?

That's how I would interpret the problem. When I work out the ratio of the masses I get a result that depends on β.

 

[Gloyn]

Oh, betha is 60 degrees. Can I see how did you work out the formula for the ratio?

 

[TSny]

Ok, I get the correct answer for β = 60^o.

Note that β is given to be the angle between the two final velocities. So, what angle should be in your equations? Your equations all look good, by the way, except you should not be using β as the angle. Instead you should use an angle related to β.

 

[Gloyn]

Oh, yeah, it should be 30 degrees, so half betha. But I only have 3 equations and 4 variables (ratio and 3 different velocities). How do I overcome this?

 

[haruspex]

But I only have 3 equations and 4 variables (ratio and 3 different velocities). How do I overcome this?

You only care about the ratio of the masses, so it will turn out that your 3 equations are enough.

 

[TSny]

The equations cannot determine values for all 4 quantities. But you can think of the three equations as equations for three unknowns: the ratio of the masses, the ratio u₁/v₁, and the ratio u₂/v₁. You can see that if you divided all three equations by m₂, the first two equations by v₁ and the last equation by v₁², you would get three equations for the 3 unknown ratios. [Edited]

You are looking for the ratio of m₁/m₂, which you can just call r. Can you express each equation in terms of r? What does the 2nd equation give you for u₂ in terms of u₁ and r?

 

[Gloyn]

Oh, I'm dumb. Thank you guys.