Calculate the angular acceleration of a hand - no time given

[BosonF]

Homework Statement

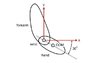
When the hand is rotating about the wrist in the sagittal plane its centre of mass has an acceleration of 3m/s(squared) in a horizontal direction, its mass is 2kg and the vertical direction (i.e. Y) is against gravity. The hand travels through 30 degrees. If the distance from the wrist joint to the centre of mass is 0.04m, what should the angular acceleration of the hand about the wrist be?
a) 17.5
b) 27.5
c) 37.5
d) 47.5

Homework Equations

angular acceleration = change in angular velocity/time

The Attempt at a Solution

To calculate the time I made an assumption that the starting velocity was 0 and the ending velocity was 3m//s. I converted the degrees to radians by multiplying by pi/180. To calculate the distance traveled in the x direction I used x= Cos30 x 0.04. So if the hand travels 3m in 1s then it travels xm in x/3 s. Which worked out as 0.034641/3 = 0.01155s.

To find the angular acceleration I then divided the radians by the time. which gave me 0.5236-0/0.01155 = 45.33 rad/s(squared)

Have I followed the correct method?

 

[CWatters]

As far as I can see there is no need to calculate a "time" or a "distance".

You are given the linear acceleration of the centre of mass (3m/s/s), the radius (0.04m) and asked to calculate the angular acceleration.

Do you know the equation that relates these three things?

 

[BosonF]

Oh, is it tangential acceleration = angular acceleration x radius?

What a relief, thank you!

 

[CWatters]

That's the equation I was thinking of but it doesn't appear to give one of the multi choice answers.

So perhaps the geometry isn't as simple as I thought. I've no idea what the sagittal plane is.

 

[BosonF]

Yes I realized it was slightly out after I calculated the answer. But then I wondered whether the radius should be the length of the hand rather than the distance to the centre of mass.

There is a table of the relative per cent of the length of the hand where the centre of mass is in the notes. I contains two values from two different people. If I take the average value I get 45.15 per cent. Using that with 0.04 gives the length of the full hand as 0.08859358 m.

Using the length of the hand as a radius I get 33.86 rad/s/s. So close to one of the answers.

Does that look right? Or have I gone off track again?

 

[CWatters]

Think that's wrong. It says that he centre of mass has linear acceleration 3m/s/s so it's the radius of the centre of mass that matters when calculating the angular acceleration. That gives an answer of 75rads/s. Perhaps the book answer is wrong?

Can you check the wording of the problem because I am wondering if they they might be asking for the acceleration in a different plane to that of the rotation? Is it a coincidence that sin(30) = 0.5 and that half of 75 is 37.5? Was a diagram provided?

 

[BosonF]

There is also a diagram included with the question. I have attached it here.

Here is the exact wording of the question:

When the hand is rotating about the wrist in the sagittal plane as shown in the figure below, its centre of mass has an acceleration of 3 m/s/s in the horizontal direction, its mass is 2kg and the vertical direction (i.e. Y) us against the direction of gravity.

If the distance from the wrist joint to the COM is 4cm, what should the angular acceleration of the hand about the wrist be?
a) 17.5 rad/s/s
b) 27.5 rad/s/s
c) 37.5 rad/s/s
d) 47.5 rad/s/s

Thank you so much for your help.

 

[CWatters]

OK all is clear. I have to go out for a few hours but will try to post a marked up drawing when I get back. Meanwhile the radius to be used in the equation is indeed 0.04*Sin(30) making the answer 37.5 m/s/s. Well at least I think so!

 

[BosonF]

Thank you

 

[CWatters]

Here is a drawing..

There is a slight change to what I said in post #8. It's Cos(60) rather than Sin(30) but this is also 0.5..

The green line shows the Linear Acceleration which the problem statement says is horizontal (3m/s).
The purple line shows the tangential component of the Linear Acceleration = 3Cos(60)

So I make the angular acceleration...

3Cos(60)/0.04 = 37.5 rads/sec

Hope I have that right as I'm a bit tired after driving my kids to rugby training.

 

[BosonF]

Thank you so much, I really appreciate your help. The drawing has really helped my understanding.