Calculate the change in the arc

[Dell]

please help urgent!

in the following question,

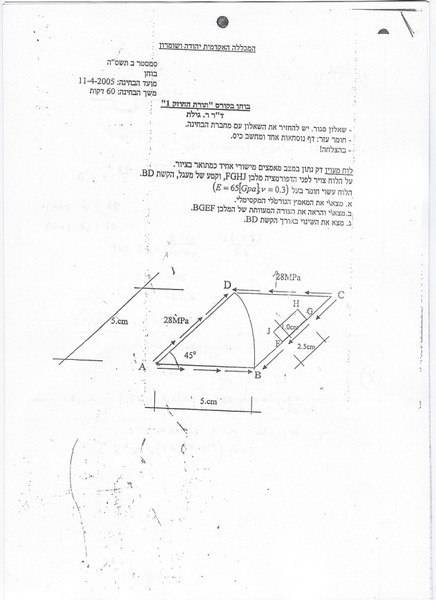
E=65 GPa
V=0.3



find the new length of the arc BD??

i have found the stresses

xx=-56Mpa
yy=0
xy=-28Mpa

using hookes law i can find the strains

xx=-8.615e-5
yy=2.58e-4
0.5*xy==-1.12e-3

but how do i calculate the change in the arc using this? i would know how to solve this if i had some kind of angular strain- i need to use a polar system not Cartesian. is there any way to do this?

also how do i know the new angle DAB? i know that the XY axis' new angle is 90.06417, and the n,t system (axes tilted 45 degrees to XY) is also 90.06417 but how do i find DAB,? generally is there any way of knowing how the axis is strained, for example, has the X axis dropped 0.06417 degrees, or the Y axis opened up 0.06417 degrees, or a bit each??
in this specific case can i say that since there is no yy strain the x-axis stays at the same angle?

DA*=DA(1+tt)=4.999569cm
AB*=5.0012923cm


can i do this:

using the transformation equations, i know

ε_nn= (ε_xx + ε_yy)/2 + (ε_xx - ε_yy)/2*cos(2ϴ) + ε_xxsin(2ϴ)

since i have already found xx, yy, xy, instead of looking for a specific ε_nn can i take the whole eqaution and say

ΔL=$$\int$$ε_nndL {dL=r*dϴ}

=$$\int$$ε_nn*r*dϴ with my integral going from 0 to pi/4

is this a possibility?


the correct answer is meant to be 2.2167e-5m

how do i know whhat my lims are for integratin, i thought maybe pi/2 -> 3pi/4 but can't get it

 

[Dell]

i tried the following logic,
since in this special specific case, i have found that $$\epsilon$$_xx = $$\epsilon$$_AD, i know that the radiiii will stay rhe same lengths as each other after deformation therefore preserving the circular shape of the arc

knowing that the volume of the shape with an area of an eighth of a circle (DAB) before deformation is V and after deformation is V'
lets say the thickness of the board is "t"

the new angle DAB is " a' " after deformation

$$\Delta$$=($$\epsilon$$_xx +$$\epsilon$$_yy + $$\epsilon$$_zz)

V=(pi*R²)t/8

V'= (a')(R')²(t')/2

but i also know that

V'=$$\Delta$$*(1+V)
R'=R(1+$$\epsilon$$_xx)
t'=t(1+$$\epsilon$$_zz)

(a')(R')²(t')=(pi*R²)t/8*(1+$$\epsilon$$_xx +$$\epsilon$$_yy + $$\epsilon$$_zz)

(a')(R(1+$$\epsilon$$_xx))²(t(1+$$\epsilon$$_zz))=(pi*R²)t/8*(1+$$\epsilon$$_xx +$$\epsilon$$_yy + $$\epsilon$$_zz)therfore i get

(a')= (pi/4)*(1+$$\epsilon$$_xx +$$\epsilon$$_yy + $$\epsilon$$_zz)/[(1+$$\epsilon$$_xx))²((1+$$\epsilon$$_zz))]

once i have the new angle, since it is still an arc of a circle

L'=R'*a'
L=R*pi/4

$$\delta$$L=L'-L

but this gives me an incorrect answer

is this a correct method and do i maybe have something wrong in y calculations

i get $$\delta$$L=1.016463761198405e-005

 

[Mene]

to work


I would suggest approaching this problem using the principles of solid mechanics and material properties. First, it is important to understand the concept of strain and how it relates to the change in length of a material. Strain is defined as the ratio of the change in length to the original length, and it can be expressed as a percentage or in decimal form. In this case, the strains in the x and y directions have already been calculated using Hooke's law.

Next, we can use the formula for angular strain to find the change in the arc. This formula relates the change in length to the radius and the angle of the arc. Since the angle of the arc is unknown, we can use the fact that the sum of the strains in the x and y directions is equal to the angular strain. This can be expressed as:

εθ = εxx + εyy

Then, using the given value of V (Poisson's ratio), we can solve for the angular strain and plug it into the formula for change in arc length:

ΔL = εθ * r

Where r is the radius of the arc. We can then use this formula to find the change in arc length for each segment of the arc (DA and AB).

To find the new angle DAB, we can use the fact that the angle between the XY and n,t coordinate systems is equal to the angle between the original and deformed axes. We can determine this angle by using the strain values in the x and y directions and solving for the angle using trigonometric functions.

As for your proposed method of using the transformation equations and integration, it may be possible to use this approach, but it would require a deeper understanding of solid mechanics and coordinate transformations. It may be more straightforward to use the method described above.

Overall, it is important to approach this problem systematically and use the principles and equations of solid mechanics to solve it. I hope this helps and good luck with your calculations.