Calculate the electric field at a given point

[fluidistic]

Homework Statement

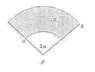
The picture describes the situation. I want to find the electric field at point P.
The charged part is a part of an annulus with interior radius a and exterior radius b.

Homework Equations

None given.

The Attempt at a Solution

I think I must integrate the electric field produced by small (differential) annulus from a to b. Wouldn't the electric field of one of them be $$\sigma A$$ where A is the area of such an annulus?
$$A=\pi ((a+dx)^2-a^2)\cdot \frac{\alpha}{\pi}$$ for the first annulus; $$\alpha$$ is the angulus shown in the figure.

 

[ideasrule]

I think I must integrate the electric field produced by small (differential) annulus from a to b. Wouldn't the electric field of one of them be $$\sigma A$$ where A is the area of such an annulus?

$$\sigma A$$ (or rather, $$\sigma dA$$) is the charge of each differential annulus, not the electric field. Remember that E=kQ/r^2, so you'll have to integrate to find the electric field due to each tiny annulus.

 

[fluidistic]

$$\sigma A$$ (or rather, $$\sigma dA$$) is the charge of each differential annulus, not the electric field. Remember that E=kQ/r^2, so you'll have to integrate to find the electric field due to each tiny annulus.

You're right! I need to reread my whole course quickly!
Thanks. I'll post my attempt as soon as I can.

 

[AEM]

I think you might be able to simplify your problem by using the inherent symmetry of the shape. Draw a line vertically through the diagram bisecting the annulus. Now consider the electric field from two bits of charge on the annulus that are located symmetrically with respect to the line and are the same distance from point P. Two of the components of the electric field at P due to these dQ's cancel, and two components add. You might want to set up a double integral that expresses this cancellation (by introducing a cosine term to project the electric field onto the vertical line) and where you represent your charge, dQ, as a little piece $$\sigma r d\theta dr$$. Then integrate from r = a to r = b and from $$\theta = -\alpha to \alpha$$.

There's another small simplification you could make to the limits in the integral due to the symmetry, though it's not necessary.

 

[fluidistic]

I think you might be able to simplify your problem by using the inherent symmetry of the shape. Draw a line vertically through the diagram bisecting the annulus. Now consider the electric field from two bits of charge on the annulus that are located symmetrically with respect to the line and are the same distance from point P. Two of the components of the electric field at P due to these dQ's cancel, and two components add. You might want to set up a double integral that expresses this cancellation (by introducing a cosine term to project the electric field onto the vertical line) and where you represent your charge, dQ, as a little piece $$\sigma r d\theta dr$$. Then integrate from r = a to r = b and from $$\theta = -\alpha to \alpha$$.

There's another small simplification you could make to the limits in the integral due to the symmetry, though it's not necessary.

I've tried your way since I made an error via my way.
If I understand you well, the double integral gives you the total charge of the annulus, but how does it matter for calculating the electric field?
I did a sketch, I realize that the horizontal components of the small dQ on each side of the vertical line cancels out. And that the vertical sum up, but I don't realize this with my draft, rather by intuition.
So $$dQ=\sigma dA$$, but thanks to calculus III we have that $$dA=rd\theta dr$$ in polar coordinates, ok I follow you. Hence $$Q=\int_a ^b \int _{-\alpha}^{\alpha} \sigma r d \theta d r=\sigma \alpha (b^2-a^2)$$.
I really need to reread my whole course...
While doing so, could you please help me a bit more?
Thanks anyway!

 

[AEM]

I've tried your way since I made an error via my way.
If I understand you well, the double integral gives you the total charge of the annulus, but how does it matter for calculating the electric field?
I did a sketch, I realize that the horizontal components of the small dQ on each side of the vertical line cancels out. And that the vertical sum up, but I don't realize this with my draft, rather by intuition.
So $$dQ=\sigma dA$$, but thanks to calculus III we have that $$dA=rd\theta dr$$ in polar coordinates, ok I follow you. Hence $$Q=\int_a ^b \int _{-\alpha}^{\alpha} \sigma r d \theta d r=\sigma \alpha (b^2-a^2)$$.
I really need to reread my whole course...
While doing so, could you please help me a bit more?
Thanks anyway!

You're on the right track BUT and this is a big BUT! You actually have to calculate the magnitude of the electric field component in the vertical direction. Remember that the dE from each bit of charge dQ is pointing at an angle from the vertical. So you don't want to compute the total charge as you did, but you need to set up the integral to compute the total electric field as in

$$E = \int \frac{1}{4 \pi \epsilon_0} \frac{1}{r^2} cos(\theta) dQ$$

Where dQ is your expression above (and my integral sign stands for your two definite integral signs).

So you will need the cosine term in your expression as well. The theta is the angle between the electri field vector and the vertical.

When I did your problem, I ended up with a $$sin( \alpha)$$ and a $$ln(\frac{b}{a} )$$ in the answer.

 

[fluidistic]

I'm sorry, I don't know why I can't do this exercise.
I've tried again and again.
I am restarting...
$$dQ=\sigma dA=\sigma r dr d \theta$$.
$$d\vec E = \frac{kdQ \hat r}{r^2}=\frac{k\sigma dr d\theta}{r}\hat r$$.
Now this is where I'm stuck.
I know that $$\hat r$$ points from the $$dA$$ element to the point P and that its magnitude is 1 but it is multiplied by a scalar (namely $$\frac{k\sigma dr d\theta}{r}$$) so I've no idea about how to plug the $$\cos \theta$$ term in the formula of $$d\vec E$$. Although I realize that the electric field at P only has a vertical component which is the sum of all the vertical components of the dA elements...
Can you help me once again, please? (By the way I also understand the limits of integration, I'm just stuck on how to introduce the $$\cos \theta$$ term; for now at least).
Thank you for having helped me so far.

 

[AEM]

I'm sorry, I don't know why I can't do this exercise.
I've tried again and again.
I am restarting...
$$dQ=\sigma dA=\sigma r dr d \theta$$.
$$d\vec E = \frac{kdQ \hat r}{r^2}=\frac{k\sigma dr d\theta}{r}\hat r$$.
Now this is where I'm stuck.
I know that $$\hat r$$ points from the $$dA$$ element to the point P and that its magnitude is 1 but it is multiplied by a scalar (namely $$\frac{k\sigma dr d\theta}{r}$$) so I've no idea about how to plug the $$\cos \theta$$ term in the formula of $$d\vec E$$. Although I realize that the electric field at P only has a vertical component which is the sum of all the vertical components of the dA elements...
Can you help me once again, please? (By the way I also understand the limits of integration, I'm just stuck on how to introduce the $$\cos \theta$$ term; for now at least).
Thank you for having helped me so far.

No problem.Here's the deal: as long as you have the unit vector r-hat in there your dE is a vector. But since you have already realized that one (the horizontal) component of the dE vectors cancel out, what you want to do is add up the other components --the vertical ones. You get them by dropping the unit r-hat vector and multiplying your expression by cos(theta) where theta is the angle between the vector dE and the vertical. It's that simple. Think back to when you first learned about vectors and they asked you "What is the x component of this vector? What is the y component of that vector? You took the length of the vector and multiplied it by the appropriate sine or cosine. Here I'm telling you it's cos(theta) as defined earlier.

 

[fluidistic]

No problem.Here's the deal: as long as you have the unit vector r-hat in there your dE is a vector. But since you have already realized that one (the horizontal) component of the dE vectors cancel out, what you want to do is add up the other components --the vertical ones. You get them by dropping the unit r-hat vector and multiplying your expression by cos(theta) where theta is the angle between the vector dE and the vertical. It's that simple. Think back to when you first learned about vectors and they asked you "What is the x component of this vector? What is the y component of that vector? You took the length of the vector and multiplied it by the appropriate sine or cosine. Here I'm telling you it's cos(theta) as defined earlier.

Thanks a lot!
I've reached $$E=2k\sigma \ln \left( \frac{b}{a} \right ) \sin (\alpha)$$. I don't know if it's the right result, but at least it makes sense if $$\alpha=\pi$$ or 0.

Thank you very much for all, you've been extremely helpful to me. Very nice explanations.

 

[AEM]

That looks like what I got. You're very welcome.