I Calculate the Resultant Force Between 4 Points

[AmateurHour]

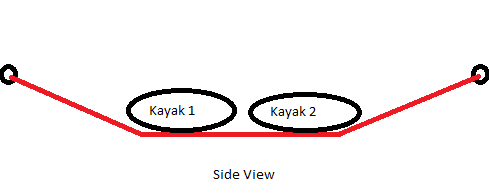
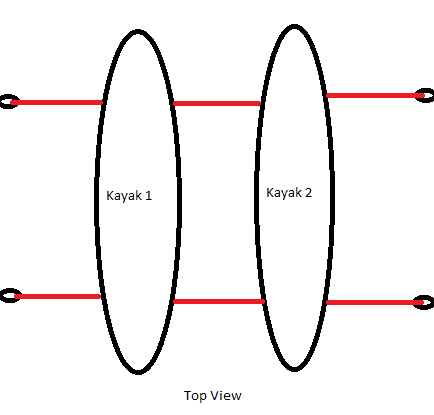
I am trying to figure out how to calculate the resultant force between 4 anchor points. Basically I want to hang two kayaks on two ropes suspended across a room. Below I have some crudely drawn images of the set up:

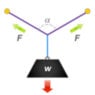
I found how to calculate the vector forces between two points as pictured below below but am wondering how it would work with four points. Is it as easy as calculating each set of two points with half the weight distributed to each set? Both kayaks should have a combined mass of less than 32kg.

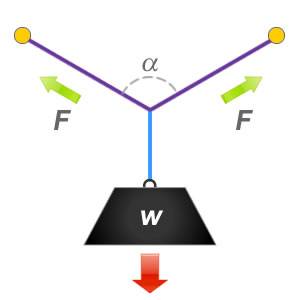
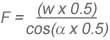
F is the resultant force exerted to each anchorage.
W is the weight of the load.
α is the internal angle between the two slings.

 

[jrmichler]

Is it as easy as calculating each set of two points with half the weight distributed to each set?

Yes, it is. Just be aware that getting the kayaks in and out of there will involve higher forces while you are pulling and tugging, and maybe jerking.

 

[AmateurHour]

Yes, it is. Just be aware that getting the kayaks in and out of there will involve higher forces while you are pulling and tugging, and maybe jerking.

Thanks!

 

[Nugatory]

Is it as easy as calculating each set of two points with half the weight distributed to each set?

The weight generally will not be evenly divided between the two ropes; you'd have to get the kayaks positioned with their centers of gravity exactly between the two ropes for an even division of the weight. Worst cas, all the weight will be on one rope while the other is doing nothing.