- #36
Viraam
- 66
- 2
You are right. No classroom door can be so small.NickAtNight said:Please let them know they have a math errors in their problem !
Question 1 geez ! Let's fix it.
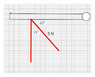
Torque = F × d
= 2 N x 0.4 m
= 0.8 N-m.
Fixes
1) The force is 2N not 20 N !
2) You put the numbers into the equation in the same order. They flipped them and put in distance force instead of Force Distance
3) the answer is 0.8 N-m not 8 N-m
Question 2 - aw man ! Question is bad.
1) why did they change the door width?
They should have left it the same for the concept they showing - moving in the Force from the doors edge
2) the fancy door handle should have wen simpler. No dividing by two. Just position the handle x distance in and be done with it. I would do a fancy handle in the third exercise, not the second.
3) they changed the force from 2 N to 5 N from the first problem, but then revert to 2N in the problem!
Let's leave the Force at 2N
Leave the width at 40 cm
Put the handle at 10 cm from the doors edge
So handle to hinges is door width less handle distance = 40 - 10 = 30 cm
So force times distance is 2 N * 0.3 m is 0.6 N-m
POINT: Oh, and are they kidding about the 'classroom' door width. Is this a classroom for midgets? How wide should a classroom door be... 36" is probably standard these days. At 2.4 cm to the inch these doors need to be 92 cm wide !