AlejandreBurgues908
- 9
- 0
Homework Statement
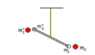
The torsion balance shown in the figure consists of a 40 cm long bar with lead balls with a diameter of 2 cm on each end. The rod is hanging by a 100 cm long silver thread with a diameter of 0.5 mm. When two bigger lead balls (density = 11.4 g/cm3) with a diameter of 30 cm are placed very close to each one of the balls, on opposite sides, their gravitational attraction tend to make the rod rotate in the same direction. What will the silver thread torsion be?
Homework Equations
F=[/B]G.m1.m2/r^2
T=r.F
Shear modulus
The Attempt at a Solution
The answer is θ = 0,00422º, but I don't know how to solve it.
Attachments
Last edited: