foode
- 4
- 0
Total Capacitance[SOLVED]
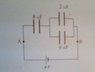
how do i calculate the total capacitance of the image attached, as there is series and parallel capacitor in the same circuit
i did try using 1/8uF + 8uF but then could not get the answer. can someone please help me through this. thanks
Homework Statement
how do i calculate the total capacitance of the image attached, as there is series and parallel capacitor in the same circuit
The Attempt at a Solution
i did try using 1/8uF + 8uF but then could not get the answer. can someone please help me through this. thanks
Attachments
Last edited: