Calculate Triangle Area with Basic Ratio Method

[SonOfGod]

This is supposed to be a simple question. However, I forgot a lot of the basics and rules I have to follow.

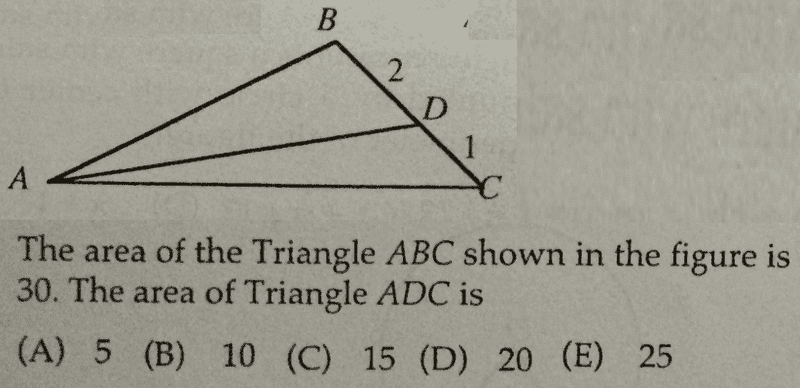
I tried to workout the height based on the area:

0.5 x 3 x h = 30
h = 20

But couldn't figure out the rest.

Then I thought about going by ratio (not from knowledge but out of desperation):

Ratio of sides: 3:1
Based on which, I assumed that the area of the triangles will follow the same ratio and therefore:

Area of big triangle : Area of small triangle = 3:1
We know that the bigger one is 30, so the smaller one has to be 10.

Answer: B.

I am correct according to the answer key. However, I just pulled that ratio thing out of my a*s. So I need someone who knows about these things to help me out so that I may "learn" instead of make stuff up.

 

[mfb]

I moved the thread to the homework section.

Just plug in the height you found (and the known base length) in the formula for the area again?

The ratio approach works as well (and saves one step), based on the same formula: area is proportional to the base length.

 

[SonOfGod]

I moved the thread to the homework section.

Sorry for the inconvenience. I should have at least read the titles of the sticky threads before posting. :P

Just plug in the height you found (and the known base length) in the formula for the area again?

Triangle ABC:

0.5x(2+1)x20 = 30

I don't know the height of the other triangle (ADC). However, since I know the answer now, I can work it out as:

0.5 x 1 x h = 10
h = 20

WHAT?! How is that even possible?!
My height calculation is messed up!

The ratio approach works as well (and saves one step), based on the same formula: area is proportional to the base length.

But I don't know if it's allowed to do that. I don't know if I can look at a triangle like that and just deduce the area of one based on the area of the other one based on the ratio of one side of the triangles.

 

[mfb]

WHAT?! How is that even possible?!
My height calculation is messed up!

Why? BC and DC are on the same line, the point A stays the same. Why should the height change?

But I don't know if it's allowed to do that. I don't know if I can look at a triangle like that and just deduce the area of one based on the area of the other one based on the ratio of one side of the triangles.

The important part is the same height for both triangles.

 

[SonOfGod]

Why? BC and DC are on the same line, the point A stays the same. Why should the height change?

The important part is the same height for both triangles.

This is what was was going on in my mind (it's wrong):

So, should the height be a line drawn from point A to the line BC? I have never seen the height line intersecting the base line without being perpendicular to the base line.

Anyway, I understand how the height has to be the same for both the triangles. However, what I still question is my ratio approach. Would that ratio approach remain fruitful for other similar triangles? I don't want to be doing the wrong thing and getting the right answer.

 

[mfb]

You take BC as base of your triangle, the red line cannot be the height you calculated. It has to be orthogonal to BC (it will meet the line at its extension beyond B).

Would that ratio approach remain fruitful for other similar triangles?

Sure (be careful with the word "similar", it has a special meaning here that you do not want).

 

[TheoMcCloskey]

hint: move that line for "height" over to the right until it intersects at point D. Visualize two triangles that it could form.

 

[SonOfGod]

hint: move that line for "height" over to the right until it intersects at point D. Visualize two triangles that it could form.

Which one of these two are you talking about:

In my first attempt, I mistakenly visualized AC to be the base. Now I understand that BC is the base. Are you talking about the option B where a straight line from the point A meets the line BC (at 90 degrees/perpendicular)?

I am more interested in the ratio of the areas of the triangles ABC and ADC. The method I used to find out the area isn't something I am confident of.

 

[mfb]

That is not 90° in option (B).

@TheoMcCloskey: I don't think the approach you suggest is helping, it is more likely to add confusion.

 

[SonOfGod]

That is not 90° in option (B).

@TheoMcCloskey: I don't think the approach you suggest is helping, it is more likely to add confusion.

lol, imagine that it intersects the line at 90 degrees. My drawing wasn't meant to be to scale. We can clearly see that its not perpendicular.

Honestly, its getting more confusing.

 

[mfb]

Do you see why the red line is the height for both triangles (with base sides BC and DC, respectively)?

 

[SammyS]

hint: move that line for "height" over to the right until it intersects at point D. Visualize two triangles that it could form.

Regarding TheoMcCloskey's suggestion:

Use the above figure along with figure A below.

Which one of these two are you talking about:

You should be able to find the ratio of the two heights .

(This is an alternative to the method presented by mfb. Don't try to combine the two.)

 

[Chestermiller]

Drop a normal from point D to side AB. In terms of angle B and side DB, what is the length of that normal? Now drop a normal from point C to side AB. In terms of angle B and side DB, what is the length of that normal?

Chet

 

[SonOfGod]

Alright, here is the way to get the same answer without using the ratio thing I did:

Since area of triangle ABC = 30,

0.5 x 3 x h = 30
h = 20

So, area of triangle ADC:

0.5 x 1 x 20
=10

 

[mfb]

Right.