- #1
Physiona
- 131
- 9
QUESTION:
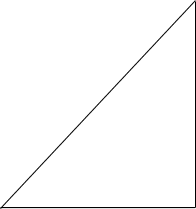

The angles in triangle ABC form an increasing arithmetic sequence.
The ratio of angles A:B:C can be written in the form 185:370:555 respectively.
You are told that the total area of the triangle is 9

Length BC is

Given the area of triangle ABC, work out the value of

Give your answer in the form
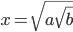 where
where
 and
and
 are integers.
are integers.
ATTEMPT:
I have decided to figure out a multiplier for all the angles provided, and labelled it as y
y(185+370+555)= 180
1110y = 180
y= 6/37
I am then planning on using the sine rule however, I don't have set values to use only angles. I'm not sure on whether or not my attempt is correct. Any guidance to helping? Thank you!
The angles in triangle ABC form an increasing arithmetic sequence.
The ratio of angles A:B:C can be written in the form 185:370:555 respectively.
You are told that the total area of the triangle is 9
Length BC is
Given the area of triangle ABC, work out the value of
Give your answer in the form
ATTEMPT:
I have decided to figure out a multiplier for all the angles provided, and labelled it as y
y(185+370+555)= 180
1110y = 180
y= 6/37
I am then planning on using the sine rule however, I don't have set values to use only angles. I'm not sure on whether or not my attempt is correct. Any guidance to helping? Thank you!
Attachments
-
 image?rev=15&h=209&w=196&ac=1.png987 bytes · Views: 964
image?rev=15&h=209&w=196&ac=1.png987 bytes · Views: 964 -
 image?rev=6&h=41&w=41&ac=1.png241 bytes · Views: 951
image?rev=6&h=41&w=41&ac=1.png241 bytes · Views: 951 -
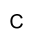 image?rev=5&h=46&w=38&ac=1.png254 bytes · Views: 924
image?rev=5&h=46&w=38&ac=1.png254 bytes · Views: 924 -
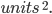 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=units%7B%5C+%7D%5E%7B2%7D.png429 bytes · Views: 913
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=units%7B%5C+%7D%5E%7B2%7D.png429 bytes · Views: 913 -
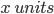 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=x%5C+units.png428 bytes · Views: 934
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=x%5C+units.png428 bytes · Views: 934 -
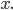 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=x.png214 bytes · Views: 939
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=x.png214 bytes · Views: 939 -
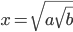 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=x%3D%5Csqrt%7Ba%5Csqrt%7Bb%7D%7D.png544 bytes · Views: 900
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=x%3D%5Csqrt%7Ba%5Csqrt%7Bb%7D%7D.png544 bytes · Views: 900 -
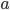 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=a.png210 bytes · Views: 944
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=a.png210 bytes · Views: 944 -
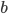 chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=b.png214 bytes · Views: 893
chart?cht=tx&chf=bg,s,FFFFFF00&chco=000000&chl=b.png214 bytes · Views: 893