Calculating Angular Speed After Spoke Shortening in Rotating System

[mandy9008]

Homework Statement

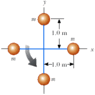
The system of small objects shown in the figure below is rotating at an angular speed of 2.0 rev/s. The objects are connected by light, flexible spokes that can be lengthened or shortened. What is the new angular speed if the spokes are shortened to 0.10 m? (An effect similar to that illustrated in this problem occurred in the early stages of the formation of our Galaxy. As the massive cloud of dust and gas that was the source of the stars and planets contracted, an initially small angular speed increased with time.)

The Attempt at a Solution

I would think that you would just multiply 2.0 rev/s by the new length, 0.10m, which will give 0.20 rev/s. When I enter this, it tells me that my answer is off by a multiple of ten.

 

[Doc Al]

Hint: What's conserved as the spokes are shortened? How does shortening the spokes affect the rotational inertia?

 

[mandy9008]

energy is conserved. sometimes it helps me when i know the answer to get to it, so i looked in the back of my textbook for a similar question. In this question, the spokes were shortened to 0.5m and the final answer was 8 rev/s. could you help me this way?

 

[Doc Al]

energy is conserved.

Actually, energy is not conserved. (It takes energy to pull in those spokes.) But something else is.

 

[mandy9008]

angular momentum is conserved?

 

[Doc Al]

angular momentum is conserved?

Yes. That's what they are looking for. (The problem is not very clearly stated.)