Calculating Area Density of Steel Discs

[bpinto]

Homework Statement

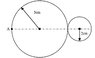
In general, the density of a three dimensional object is expressed as mass per unit volume. However where an object is of uniform thickness its depth can be combined with the density factor allowing the density to be expressed in terms of mass per unit area. A pair of steel disks joined together are of uniform thickness and each has an area density of 10 grams/cm²

Homework Equations

ρ = m/A

The Attempt at a Solution

Mass of bigger disc
10 = m/25∏

Mass of smaller disc
10 = m/4∏

Total mass = 290∏

I don't have any idea what I am doing wrong as the answer is suppose to be 58∏

 

[SteamKing]

Your calculation of the mass seems to be correct. Is your problem statement complete?

 

[bpinto]

Sorry it is incomplete I thought it was part of the attachment, the actual question asks:

What is the mass of the whole object?

 

[CWatters]

I agree. Your calculation for the total mass looks right but was that the question?

You wrote...

Mass of bigger disc
10 = m/25∏

That's correct but to me it's a slightly a strange way to do it. I would write:

Mass = area * area density

= 25∏ * 10
= 250∏

 

[haruspex]

Looks like it was supposed to be 2g/cm²

 

[bpinto]

thanks for the help guys