amanda_
- 9
- 0
Not quite sure how central angles ended up in a PreCalc class, but oh well.
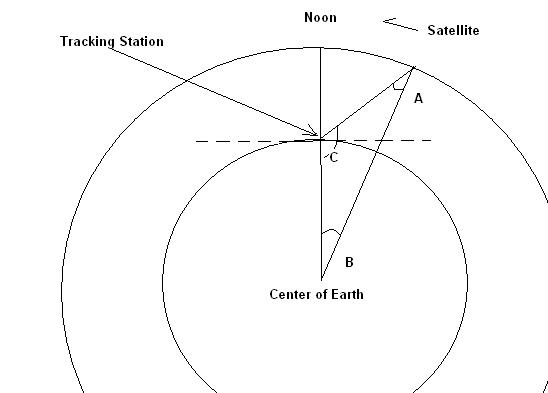
Okay so, I'm given this picture
And this information:
A satellite is in orbit 2000 kilometers above the Earth.
It is scheduled to pass directly over a tracking station at noon.
The satellite takes 2 hours to make one orbit.
The tracking antenna is aimed 30º above the horizon.
The problem is:
The central angle defines the arc of the satellite's movement from the 30º point to a point overhead. If you find the central angle, you can compute the time it takes the satellite to travel the arc of the orbit. The measure of the central angle is ____ .After having someone already try to explain this to me, I used the law of sines and cosines and ended up with this equation. Everything is starting to look all the same and I'm just getting so frustrated. Any help would be appreciated.
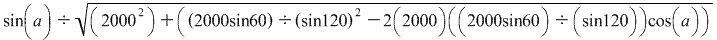
I plugged in 120 for sin a and cos a, and the whole thing comes out to be zero. Which isn't one of the possible answers.
Okay so, I'm given this picture
And this information:
A satellite is in orbit 2000 kilometers above the Earth.
It is scheduled to pass directly over a tracking station at noon.
The satellite takes 2 hours to make one orbit.
The tracking antenna is aimed 30º above the horizon.
The problem is:
The central angle defines the arc of the satellite's movement from the 30º point to a point overhead. If you find the central angle, you can compute the time it takes the satellite to travel the arc of the orbit. The measure of the central angle is ____ .After having someone already try to explain this to me, I used the law of sines and cosines and ended up with this equation. Everything is starting to look all the same and I'm just getting so frustrated. Any help would be appreciated.
I plugged in 120 for sin a and cos a, and the whole thing comes out to be zero. Which isn't one of the possible answers.
Attachments
Last edited: