Calculating Centre of Mass for a Projectile Nose

[tuoni]

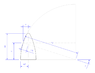
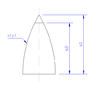
I am trying to find the centre of mass of a projectile nose. I profoundly suck at integration, but I have managed to work out area, and now I'm battling centre of mass. Am I doing this correctly? Is my final integral correct?

$$x = \sqrt{r_{1}^{2} - y^{2}} - (r_{1} - s_{2})$$

$$\int{x \;\delta y} = \frac{y}{2}\sqrt{r_{1}^{2} - y^{2}} + \frac{r_{1}^{2}}{2} \cdot \tan^{-1} \left( \frac{y}{\sqrt{r_{1}^{2} - y^{2}}} \right) - y(r_{1} - s_{2})$$

$$\delta V = 2 \pi \int{x \;\delta y}$$

$$s_{"centre"} = \frac{\rho}{m} \int{x \;\delta V} = \frac{2 \pi\rho}{m} \int{x^{2} \;\delta y}$$

 

[betel]

Your formula for the center of mass is not quite correct. You have to remember you deal with three dimensional vectors.

$$\vec s_{center} = \int \vec r dV$$

For symmetry reasons you will see at once that the center of mass has to be on the axis, i.e only $$s_y$$ is non zero.

Then you can use your integral from before. Actually this integral will be easier than the one for the total Volume.

I get
$$s_y = 2 \pi \frac{\rho}{m}\left(\frac{1}{3} r_1^3 -\frac{1}{3}\sqrt{r_1^2-s_1^2}^3+(s_2-r_1) s_1\right)$$

 

[tuoni]

Thanks for the help! I always use wolfram alpha (always get it wrong when I try it manually) so could you give me the intermediate steps (or the essential ones)?

What did you integrate to get final definite equation?

I am making generic formulas for finding volume, centre of mass, angular mass, etc., of circular cones: x(y) being the function of the cone slope, s1 being the maximum possible length of the cone (where the slope intersects the y-axis), and s2 the truncated length (and also truncated at the bottom, but not displayed here: simply int B - int A; where A is 0 for no bottom truncation).

So given x(y), what is the indefinite integral you used to arrive at your final equation?

P.S. I'm sorry if I'm asking a little too basic question :/

 

[betel]

Your way to integrate is correct. I do it the same way. I just think you got the formula for the center of mass wrong. We have to sort this one out before we can tackle the integrals.
Could you post your formula for the center of mass of a general body? Then we can check.

 

[tuoni]

Your way to integrate is correct. I do it the same way. I just think you got the formula for the center of mass wrong. We have to sort this one out before we can tackle the integrals.
Could you post your formula for the center of mass of a general body? Then we can check.

Hmm...as it is an axisymmetric body, only sy is non-zero, and as it is also has homogeneous density and continuous distribution, I thought it was:

$$R = \frac{1}{m} \int{\rho(r) r \;\; \delta V}$$

 

[betel]

For an axissymmetric body this is ok. I suspect you will enter the wrong quantity for r.
What would your formula be for a general (homogeneous) body be?

 

[tuoni]

For an axissymmetric body this is ok. I suspect you will enter the wrong quantity for r.
What would your formula be for a general (homogeneous) body be?

Had to do a little searching to make sure I got this right; so for a general body with homogeneous density the centre of mass is equal to its centroid? ...and the formula I found for this is:

$$C = \frac{\int xg(x) \delta x}{\int g(x) \delta x}$$

The old and tried formula:

$$R = \frac{\sum m_{i}r_{i}}{\sum m_{i}}$$

; but that's only for a system of bodies with COM already known for each object.

Or is the problem that I'm not using a vector form of the formulas? I haven't really found any other formulas, and not even my mathematics reference book lists any other form of general formula for COM...

 

[betel]

Usually one would write it in vector form to kkep confusion away. But we can also write it in components.
In Your notation you just have to remember that there are three C's (R's) and the x has to be chosen correspondingly.
The complete formula is
$$R_x = \frac{\int x\rho(x,y,z) dV}{\int \rho(x,y,z) dV}$$
$$R_y = \frac{\int y\rho(x,y,z) dV}{\int \rho(x,y,z) dV}$$
$$R_z = \frac{\int z\rho(x,y,z) dV}{\int \rho(x,y,z) dV}$$
For a homogeneous body $$\rho$$ will be independent of the coordinates.
For our axissymmetric body as you correctly said we only need the y-component, so we have
$$R_y = \frac{\rho}{m}\int y dV$$
Now you can split the integral the same way you did before.
And try to do the resulting integral by hand. It is really easy.

 

[tuoni]

Usually one would write it in vector form to kkep confusion away. But we can also write it in components.
In Your notation you just have to remember that there are three C's (R's) and the x has to be chosen correspondingly.
The complete formula is
$$R_x = \frac{\int x\rho(x,y,z) dV}{\int \rho(x,y,z) dV}$$
$$R_y = \frac{\int y\rho(x,y,z) dV}{\int \rho(x,y,z) dV}$$
$$R_z = \frac{\int z\rho(x,y,z) dV}{\int \rho(x,y,z) dV}$$
For a homogeneous body $$\rho$$ will be independent of the coordinates.
For our axissymmetric body as you correctly said we only need the y-component, so we have
$$R_y = \frac{\rho}{m}\int y dV$$
Now you can split the integral the same way you did before.
And try to do the resulting integral by hand. It is really easy.

Heh, nothing is that easy when you barely grasp the basics of it :) So often do I regret not taking advanced maths in college, didn't seem useful at the moment, but damn could I have used it later on!

So far I've learned what little I know from the few practical examples I've found and a few other references. I do have a few books (or rather very heavy tomes), but I guess it's rather strained when I never really learned the basics before...and maths isn't my stronger point :(

Anyway...

$$x(y) = \sqrt{r_{1}^{2} - y^{2}} - (r_{1} - s_{2})$$

$$\delta V = \int A(y) \;\;\delta y = \pi \int x(y)^{2} \;\;\delta y$$

$$\delta R_{y} = \frac{\rho}{m} \int y \;\;\delta V$$

...am I correct so far? And this in turn becomes...

$$\delta R_{y} = \pi \frac{\rho}{m} \int y \cdot x(y)^2 \;\;\delta y$$

...or would it need to be y(x)? Seems a little redundant...

P.S. I slightly change the equation to use method of disks, handy little thing I just learned. Seemed more logical to me.

 

[betel]

Sorry if I was a bit short before. I wanted to give the chance to get the details yourself.

What you say is correct. You can write either x(y) or y(x), which one you choose doesn't matter, you only have to keep the correct limits and integrations. In this case x(y) is much easier.

Actually I just noticed that we both forgot a factor of x in our earlier posts. Now your formula for the Volume is correct.

I will write a complete calculation in the next post.

 

[betel]

The volume element is
$$dV = dx\ dy\ dz$$
In our case of an axissymmetricb body it is best to use polar coordinates. In these the volume element is (in your choice of names)
$$dV= xd\phi dxdy$$
The factor xcomes from changing the volume element of integration. Probably you are more familiar with the formula written in r and $$\phi$$ in which case it is $$dxdz=rdrd\phi$$
Then the total Volume is
$$V = \int_0^{2\pi} d\phi\int_0^{s_1} dy \int_0^{r(y)} dx x$$
Now we can do the integration of the angle which will give a factor 2Pi and the integration for x. This leaves
$$V = 2\pi\int_0^{s_1} \frac{1}{2} x(y)^2 dy$$
This integral is nasty to do by hand but fortunately the integral for the center of mass will be easier.

The y-component of the center of mass is given by
$$R_y= \frac{\rho}{m}\int_0^{2\pi} d\phi\int_0^{s_1} dy \int_0^{r(y)} dx\ x\ y$$
Again as before this gives
$$R_y=\frac{\pi\rho}{m}\int_0^{s_1}dy\ x(y)^2y$$
Inserting the formula for x we get
$$R_y=\frac{\pi\rho}{m}\int_0^{s_1}dy\ y\left(r_1^2-y^2-2(r_1-s_2)\sqrt{r_1^2-y^2}+(r_1-s_2)^2\right)$$
Expanding the bracket, multiplying and simplifying we get.
$$R_y=\frac{\pi\rho}{m}\int_0^{s_1}dy\ \left(y(2r_1^2-2r_1s_2+s_2^2)-2(r_1-s_2)y\sqrt{r_1^2-y^2}-y^3\right)$$
Now you can evaluate this integral in your favourite program or do it by hand.

The first term is proportional to y, so the integral will give y^2/2. The last prop. to y^3, so integrating gives y^4/4. The middle term looks nasty because of the square root but the additional factor of y in front saves us. You will notice that
$$\int y\sqrt{r_1^2-y^2} dy = -\frac{1}{3}\sqrt{r_1^2-y^2}^3$$

Altogether we have
$$R_y=\frac{\pi\rho}{m}\left[\frac{y^2}{2}(2r_1^2-2r_1s_2+s_2^2)+\frac{2}{3}(r_1-s_2)\sqrt{r_1^2-y^2}^3-\frac{y^4}{4}\right]_0^{s_1}$$
At the lower limit this is zero. The upper limit gives your desired value.

 

[betel]

P.S. I slightly change the equation to use method of disks, handy little thing I just learned. Seemed more logical to me.

That's exactly what you need in the axissymmetric case. It gives you the additional factor x. I was to quick in my first post and forgot to include it.

 

[tuoni]

Great! Thank you very much for the help!

I've been going through the equations plenty of times and made it work for all the other shapes and forms as well. It also works in octave and mathcad. I also managed to work out moment of inertia now, and a few other things.

Thanks a lot!