Calculating Deceleration Using Calculus

[shableep]

A friend of mine lead me to this math example when I asked him what math would be involved in finding the deceleration necessary to stop an already accelerated object over a certain distance. For example, a car going 50mph that must stop in 40ft.

This was the example...

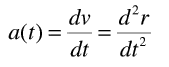
...and I have no idea where to start. Could anyone help me interpret this? And... sorry about bugging you guys with my general lack of physics understanding.

 

[LCKurtz]

Do you know calculus? If you want to stop with a constant deceleration a start with

x''(t) = -a and integrate twice to get position as a function of a and t. Set the initial velocity to 50mph (in feet per second²), initial position x = 0 and require the velocity is 0 when x = 40. Solve for a.

 

[shableep]

Thanks, LCKurtz. And no, I don't know calculus =( And while I'm sure this is probably infinitely useful, I unfortunately don't know what it is to integrate twice. It's looking like I might be in over my head and I should look into some good calculus books.

Thanks again for the help.

 

[LCKurtz]

Well, yes you will need calculus to solve that kind of problem, although some non-calculus physics books may give you the formulas without deriving them. You can do constant velocity problems with algebra using d = rt, but variable speed requires calculus. Early editions of calculus books are available cheap. You don't need the latest ones.