bbd001
- 6
- 0
NO TEMPLATE BECAUSE ORIGIONALLY SUBMIIED TO NON-homework forumHi,
I have a pipe connects to a container's outlet. The container contains water and the pipe is open-ended. When a 10Kg object is placed inside the container and compress the water. Can you tell me how to calculate the displacement of X and Y? What principle or formula should I use?
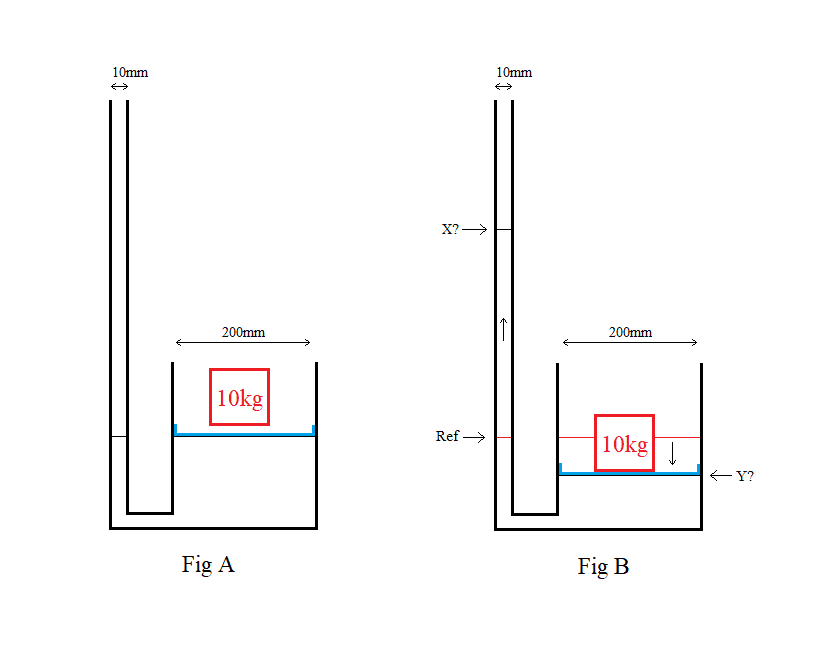
Thanks,
I have a pipe connects to a container's outlet. The container contains water and the pipe is open-ended. When a 10Kg object is placed inside the container and compress the water. Can you tell me how to calculate the displacement of X and Y? What principle or formula should I use?
Thanks,
Last edited by a moderator: