SodaBiscuit
- 4
- 0
I want to learn how to calculate what distance a fluid will travel up a small tube if a large piston is used on one side, and no piston on the other side.
Example Diagram
(Consider everything is square instead of round, for easier measurements.)
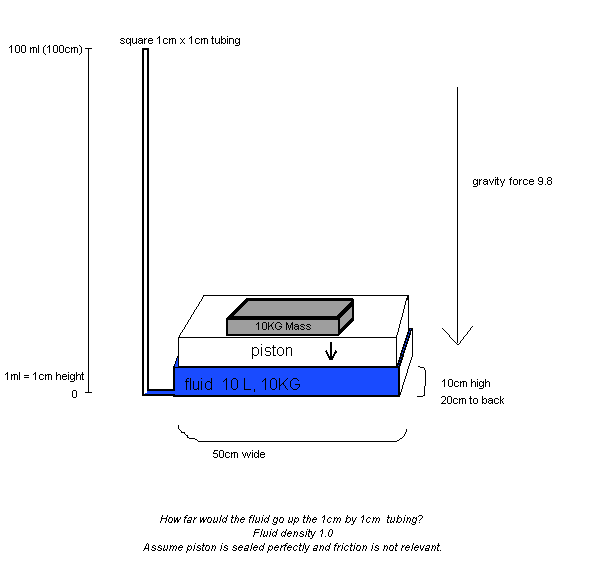
Assume there is a 10kg mass placed on a square piston.
Under the piston is 10L of water, 1.0 density, 10KG. The 10L water is spread out very wide. The piston (barrel) is 50cm wide, 20cm long, 10cm high. Assume the piston is near zero weight and the 10kg (100N) is all that is acting.
Gravity is in effect.
A 1cm by 1cm tube comes out at the very bottom of the water chamber. The tube heads up 1 meter high (100cm, 100mL volume).
If the 10kg mass is let go right there on the piston, how far up would the water go.
Forget atmosphere pressure if it makes it much simpler.
Assume the tube is open to air at the top, not closed (sorry for the crumby drawing).
A picture is attached to make it easier to visualize.
This is a problem I made up myself, just to understand how to calculate this sort of situation. It is not homework (someone moved it to the homework section for some reason). It is just a brain exercise to learn more about pistons when they push fluid in an open system.
I figure that if there is 0-100ml of water on one side maximum at any point in time, then the formula to calculate that side of the system may be p=pgh. Whereas on the piston side the formula is p=f/a.
Since this is an open system, the pressure is dynamic rather than static though.
Gravity is working on both sides of the system.
If it were a column of water on each side, which is not the case in this example, the water in the tube would simply level out per p=pgh. However in this case, shown above, I am unsure what will happen. Help me understand?
Example Diagram
(Consider everything is square instead of round, for easier measurements.)
Assume there is a 10kg mass placed on a square piston.
Under the piston is 10L of water, 1.0 density, 10KG. The 10L water is spread out very wide. The piston (barrel) is 50cm wide, 20cm long, 10cm high. Assume the piston is near zero weight and the 10kg (100N) is all that is acting.
Gravity is in effect.
A 1cm by 1cm tube comes out at the very bottom of the water chamber. The tube heads up 1 meter high (100cm, 100mL volume).
If the 10kg mass is let go right there on the piston, how far up would the water go.
Forget atmosphere pressure if it makes it much simpler.
Assume the tube is open to air at the top, not closed (sorry for the crumby drawing).
A picture is attached to make it easier to visualize.
This is a problem I made up myself, just to understand how to calculate this sort of situation. It is not homework (someone moved it to the homework section for some reason). It is just a brain exercise to learn more about pistons when they push fluid in an open system.
I figure that if there is 0-100ml of water on one side maximum at any point in time, then the formula to calculate that side of the system may be p=pgh. Whereas on the piston side the formula is p=f/a.
Since this is an open system, the pressure is dynamic rather than static though.
Gravity is working on both sides of the system.
If it were a column of water on each side, which is not the case in this example, the water in the tube would simply level out per p=pgh. However in this case, shown above, I am unsure what will happen. Help me understand?
Attachments
Last edited:
