Calculating Fgrav at a non-point mass

[diminion]

Homework Statement

Hello! I signed up about week ago, in case i needed some help in physics, and today i do. I Hope someone can explain this to me a little better.

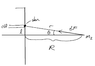
Anyways, yesterday we started the chapter on gravitation. Our professor layed out eight steps we should follow to calculate the F_grav at a non-point mass. They were,

1. Draw a diagram
2. Pick a small chunk (dm)
3. Draw a line from dm to the 2nd mass
4. Draw a force vector starting at the 2nd mass
5. Calculate dF created between dm and the 2nd mass
6. Check symmetry
7. Calculate remaining components of dF
8. Integrate

Homework Equations

He gave us the following:

dF\ =\ G\frac{dm M_{2}}{r^{2}}

Which he broke down into components,

dF_{x}\ =\ G\frac{dm M_{2}}{r^{2}}cos\theta

and

F_{y}\ =\ 0 by symmetry.

The Attempt at a Solution

When i went home, i proceeded to find dF_x
dm\ =\lambda dl

\lambda\ =\frac{M}{L}

r\ =\sqrt{(R^{2}+l^{2})}


cos\theta\ =\frac{R}{\sqrt{(R^{2}+l^{2})}}

dF_{x}\ =\ G\frac{\lambda dl M_{2}}{(R^{2}+l^{2})}\frac{R}{\sqrt{(R^{2}+l^{2})}}


F_{x}\ = \int dF_{x}\ =2\int^{\frac{L}{2}}_{0} \ G\frac{\lambda dl M_{2}}{(R^{2}+l^{2})}\frac{R}{\sqrt{(R^{2}+l^{2})}}

F_{x}\ = 2 \ G\lambda M_{2}R\int^{\frac{L}{2}}_{0}\frac{dl} {(R^{2}+l^{2})^{\frac{3}{2}}}

Now to finish this up, it seems to me like trig substitution. Is that the correct way to proceed with he integral?
My main question that i don't understand is, What does he mean "by symmetry"? I first assumed he was going to use sin\theta for F_y but he didnt. Why is F_y=0?
Thanks for any help you can give me about the symmetry part.

 

[Doc Al]

My main question that i don't understand is, What does he mean "by symmetry"? I first assumed he was going to use sin\theta for F_y but he didnt. Why is F_y=0?
Thanks for any help you can give me about the symmetry part.

Since M₂ is symmetrically located with respect to your extended mass, the y-components of force from the upper half will be exactly equal and opposite to the y-components from the lower half. Thus, "by symmetry", you know they will cancel out. Of course you can certainly work it out using sinθ, but you'll get the same answer.

 

[diminion]

Oh, i see that. Thanks for that clarification!