subbby
- 22
- 0
This is a work related problem. I was calculating the amount of force required to hold a cylinder in a position when its Center of gravity is not at the center.
Problem Background
To find :
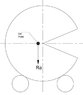
Find Pt in Picture1 (Pt is the counter force)
Given Data:
• Bigger Circle : Gear
• Smaller Circle : pinion
• Center of Gravity CG point is 14.125 inches to the left from the vertical center line
• Radius of Gear = 144”
• Radius of pinion = 10.75”
• Reactions Rb and Rc are supports. Angle Rb-O-G = Angle Rc-O-G= 30 degrees
• Ra=1,111,887.5#
Attempt 1:
Implies, Pt= (1111887.5*14.125)/144= 109065.3 #
My Doubts :
Problem Background
- Assume a 60' long cylinder.
- Circumferential it is made of 8 sections.
- For maintenance purpose, one section is completely removed (Side View shown in Picture3 & front view shown in Picture2). Hence the shift in center of gravity. (Shown in Picture2)
- This entire arrangement is rotated with the help of gear and pinion arrangement. (Picture1.)
To find :
Find Pt in Picture1 (Pt is the counter force)
Given Data:
• Bigger Circle : Gear
• Smaller Circle : pinion
• Center of Gravity CG point is 14.125 inches to the left from the vertical center line
• Radius of Gear = 144”
• Radius of pinion = 10.75”
• Reactions Rb and Rc are supports. Angle Rb-O-G = Angle Rc-O-G= 30 degrees
• Ra=1,111,887.5#
Attempt 1:
- Finding moments about point O.
- Therefore since direction of reactions Rb and Rc are in the line of action of force, they wouldn't have any moment about the point ‘O’ …. Correct me if I am wrong
Implies, Pt= (1111887.5*14.125)/144= 109065.3 #
My Doubts :
- Is this approach correct ? and is this the value of the force required to hold the cylinder
- Or do I have to consider the reactions Rb and Rc too ? If that is the case I shall end up having three unknowns, namely Rb,Rc and Pt.