Calculating Horizontal Acceleration on 7.20 kg Block w/F1 & F2

[dragon18]

Two forces, F1 and F2, act on the m = 7.20 kg block shown in the figure below.

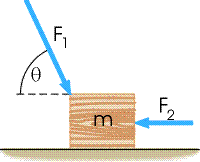
The magnitudes of the forces are F1 = 56.8 N and F2 = 39.2 N. θ = 70.4°. What is the magnitude of the horizontal acceleration of the block?

Relevant equations
V_0x=v₀cosθ
V_0y=v₀cosθ
F=ma


The attempt at a solution
Too many to list

 

[Bostonpancake0]

Before you can calculate the net horizontal acceleration, you need to find the net Horizontal force on the block. then Newtons second law should work to give you the net horizontal acceleration.

 

[haruspex]

I've seen better worded questions. Since the block appears against a fixed surface (a table?), I'd guess there's a third force (and a fourth if there's gravity). And you just have to assume there are no more unmentioned forces, such as friction.

 

[dragon18]

F1=56.8 N
F2=39.2 N
Weight of the block is 70.56, so the force the table is exerting upward on the block is 70.56 N.

So the net force is 166.56N?

I know that if I divide that by the mass, I will not get the correct answer.

So what's next?

 

[haruspex]

Weight of the block is 70.56, so the force the table is exerting upward on the block is 70.56 N.

No. Resolve each force on the block into its horizontal and vertical components. What do you get? What are the accelerations in those directions (using unknowns where appropriate)? So what equations can you write
(Actually, you'll find you don't need to worry about the vertical direction at all, but let's do this thoroughly.)

 

[dragon18]

No. Resolve each force on the block into its horizontal and vertical components. What do you get? What are the accelerations in those directions (using unknowns where appropriate)? So what equations can you write
(Actually, you'll find you don't need to worry about the vertical direction at all, but let's do this thoroughly.)

I got 13.15N for the horizontal and 53.50N as the vertical. I don't really know if those are correct and I don't understand what to do afterwards.

 

[haruspex]

I got 13.15N for the horizontal and 53.50N as the vertical.

That's just adding up the forces in the diagram, right? But as I mentioned, the normal force is missing. What will the acceleration be in the vertical direction? What does that tell you about the normal force?
Given that there are no other horizontal forces, what will the horizontal acceleration be?

 

[dragon18]

In the vertical direction I got 1.91 m/s^2 for acceleration. I think the horizontal acceleration in 5.44 m/s^2.

I am sorry, I'm just very bad at following written directions

 

[haruspex]

In the vertical direction I got 1.91 m/s^2 for acceleration. I think the horizontal acceleration in 5.44 m/s^2.

Horizontal sounds about right. For vertical, how is the block going to accelerate through the table?