Calculating Induced EMF and Current in a Moving Rod in a Magnetic Field

[purduegirl]

Homework Statement

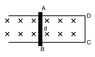
A conducting rod AB of length d = 1.8 m makes contact with the metal rails AD and BC as shown in the diagram. The apparatus is in a uniform magnetic field of flux density 680 mWb / m2, perpendicular to the plane of the diagram.

1) Find the magnitude of the induced emf in the rod if it is moving to the right with a velocity of 1 m/s.

2) If the resistance in the circuit is 1.8 Ω, calculate the magnitude of the induced current.

3) Find the rate at which heat is developed in the circuit.

4) Now, instead of a normal magnetic field, the magnetic field makes an angle of 60° with the plane of the loop ABCD. Find the induced emf for the same flux density and velocity.

Homework Equations

1) Flux = B*A*cos \vartheta.
E = vBL

2) Not sure, couldn't find any equations to use in my book for these.

The Attempt at a Solution

1) I'm having trouble trying to solve for B. The equation I was given was B = Force/qvSin\vartheta. I know the flux, so I thought I'd solve for B. But, without knowing the length of the rectangle, I can;t find the area thus giving me two variables. Any help on this problem would be greatly appreciated.

 

[dynamicsolo]

Your attachment probably won't come up for some while, but the problem set-up is familiar.

Magnetic flux density is B, the units for which are expressed as Webers/(m^2) = Teslas [ Wb/(m^2) = T ]. So you are already given B in the problem statement. What you are solving for in part (1) is the rate of change of flux through the expanding loop enclosed by the end, the rails, and the moving bar. The magnetic field is perpendicular to this loop, so what is cos(theta) equal to?

As for part (2), you will find the induced emf (which has units of volts) in part (1). You are given a resistance for the loop. How do you find current from a known voltage?

 

[purduegirl]

For part one, cos theta would be equal to 90 degrees if it is the angle for a perpendicular angle, right?

 

[dynamicsolo]

Well, here's the thing: the area of a loop has a vector A assigned to it that is perpendicular to its face. So, in the convention used for these calculations, the magnetic field B is perpendicular to the loop, but parallel or anti-parallel to A. So \theta is taken to be either 0º or 180º; it won't matter which, though, for finding the magnitude of the induced emf.

 

[purduegirl]

3) Find the rate at which heat is developed in the circuit.

This part I am not sure about. I tried to find an equation in my book, but didn't

4) Now, instead of a normal magnetic field, the magnetic field makes an angle of 60° with the plane of the loop ABCD. Find the induced emf for the same flux density and velocity.

But, I'm not sure where the angle comes in. I thought at first I would have to calculate new flux, but it says not to. Any ideas?

 

[dynamicsolo]

For (3), this may be referred to in your book as "power dissipated by a resistor". What is the power dissipated (converted into "internal energy") by a resistance R with a current I flowing through it?

In (4), the magnetic field is now tilted 60º to the plane of the loop, rather than 90º (perpendicular) as it was for the first three parts. What will the angle theta[\tex] be this time?

 

[purduegirl]

For part three, I found the equation of Pav = 1/2IV or 1/2I^2R.

Using Pav = 1/2I^2R = 1/2(.68 A)^2(1.8 Ohms) = 0.41616 W
Using Pav = 1/2IV = 1/2(.68 A)(1.22V) = 0.4148 W

Neither of these work.

 

[dynamicsolo]

For part three, I found the equation of Pav = 1/2IV or 1/2I^2R.

Using Pav = 1/2I^2R = 1/2(.68 A)^2(1.8 Ohms) = 0.41616 W
Using Pav = 1/2IV = 1/2(.68 A)(1.22V) = 0.4148 W

Neither of these work.

EDIT: OK, skip the comment I had here a minute ago. I don't know what passage you found that equation in, but that is an average power for whatever situation they are describing. The equation for the power dissipated by the resistance won't have that factor of 1/2. It should just be P = VI = (I^2)·R .

Another way of getting at this is that the moving bar must be pushed by an applied force, but only moves at constant velocity. So there is a resisting force also acting on this conducting bar. That is the magnetic force acting on the current flowing through the bar (the source of this current is from the magnetic induction), given by

F = IL x B ,

which, since the current is flowing perpendicularly to the magnetic field, has a magnitude of

F = ILB sin(90º) = ILB · 1 .

The power exerted on the bar by this resisting magnetic force is

P = F · v = Fv cos(180º),

since the magnetic force points in the opposite direction to the bar's velocity (well, that's what makes it a "resisting" force). The power comes out negative because it is dissipating mechanical energy (it is a non-conservative force). The magnitude of this power is then

P = (ILB) · v
= (0.68 A) · (1.8 m) · (0.68 Wb/(m^2)) · (1 m/(sec^2)) = 0.832 W .

The energy is dissipated as heating, much as is done by familiar surface friction. (That is why this process is also referred to as "magnetic drag" or "magnetic damping".) You get the same result from calculating the power dissipated by the 1.8-ohm resistance.

 

[purduegirl]

Well that explains why I couldn't get the right numbers, I don't have that equation in my book.

For part 4,

All I need to find is the magnetic field which would follow the formula B = \sqrt{\frac{F}{qvSin\theta}}

V and theta are given.
But, I an given no indication of what the charge is and how to calculate the force.

 

[alphysicist]

Hi purduegirl,

Well that explains why I couldn't get the right numbers, I don't have that equation in my book.

For part 4,

All I need to find is the magnetic field which would follow the formula B = \sqrt{\frac{F}{qvSin\theta}}

V and theta are given.
But, I an given no indication of what the charge is and how to calculate the force.

I think a better starting point would be the emf formula you have listed in your original post. However, to handle the angle, you would probably want to look in your textbook and find out what it says about that formula. I think it should either list an assumption about B, L, and v; or it perhaps might have said that the B in that equation is just a particular part of the total magnetic field. However it derives that formula, how would you handle the angle?

 

[dynamicsolo]

Refer back to post #4. Now, B is making an angle of 60º to the plane of the loop, while A is defined to be 90º to the plane of the loop. So what is the angle between B and A, which is theta?

 

[purduegirl]

Would the angle be 30 degrees?

 

[alphysicist]

Would the angle be 30 degrees?

That sounds right to me. What does that give?