matematikuvol
- 190
- 0
\oint_S \vec{A}\cdot d\vec{S}=\int_V div\vec{A}dv
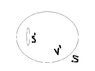
Suppose region where \vec{A}(\vec{r}) is diferentiable everywhere except in region which is given in the picture. Around this region is surface S'. In this case Gauss theorem leads us to
\int_S \vec{A}\cdot d\vec{S}+\int_S \vec{A}\cdot d\vec{S}=\int_{V'} divAdv
Am I right?
Suppose region where \vec{A}(\vec{r}) is diferentiable everywhere except in region which is given in the picture. Around this region is surface S'. In this case Gauss theorem leads us to
\int_S \vec{A}\cdot d\vec{S}+\int_S \vec{A}\cdot d\vec{S}=\int_{V'} divAdv
Am I right?
Last edited: