Calculating K-Work on Box with θ=30° Inclined Board & Mass

[chrisfnet]

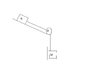
We recently did a lab with an inclined board and a box connected to a hanger with mass (over a pulley).

I've gotten all of the calculations I need except for two. I was wondering if I could get a little help.

When θ = 30°, what was the k-work done on the box by the suspended weight when the box moved (a) up the incline and (b) down the incline?
When θ = 30°, what was the k-work done on the box by gravity when the car moved (a) up the incline and (b) down the incline?
(a) For the box going up the incline, what percentage of the k-work done by the suspended weight is lost to friction? (b) For the box going down the incline, what percentage of the k-work done by gravity is lost to friction?

Theta is the angle of inclination. The displacement would be 0.218m. The suspended mass was 0.190kg to allow the box to move up the incline. The mass was 0.053kg to allow the box to move down the incline.

Any help would be greatly appreciated.

 

[Vykan12]

First, you should know that

f_{k} = u_{k} n

Where f_{k} is the force of kinetic fricition, u_{k} is the coefficient of static friction and n is the normal force of the object in question.

So w_{k} = f_{k}*d*cos(theta) = u_{k}*n*d*cos(theta)

Where w_{k} is work of kinetic friction, d is the displacement of the object and theta is the angle between the force and displacement vectors.

To find the amount of energy lost to friction, find the gravitational potential energy of the object before it was released and find the kinetic energy of the object once it reaches the bottom of the incline. Taking the difference of those two values will give you your answer.

I recommend drawing a free body diagram for these calculations.

 

[chrisfnet]

So when I use wk = fk*d*cos theta I get the work done by friction on the box, but I need the work done on the box by the suspended weight.

 

[Vykan12]

The suspended weight will simply have a different normal force due to having a different mass (in all likelihood you'll have n = m*g*trigfunction(theta) ).

 

[chrisfnet]

So I need the tension force, don't I? The tension force * displacement would equal the work, no?

 

[chrisfnet]

I've been trying to set this up all day, could anyone please help with these?

 

[Vykan12]

I made a rough sketch of what I think your experiment looks like. I need you to check that it's an accurate representation before I can help you further.

 

[chrisfnet]

I made a rough sketch of what I think your experiment looks like. I need you to check that it's an accurate representation before I can help you further.

Awesome, thanks. Awaiting approval... argh. Who knows how long that'll take, haha.