Calculating Minimum Values for Artificial Gravity in Centripetal Force Wheels

[julianwitkowski]

Hey thanks for reading:)

I'm trying to learn calc and I thought it would help if I could figure out how to do this...

For school I have a physics paper on artificial gravity and how it could work... I didn't post this in HW help because It's more of a written thing and I just got sidetracked by boredom.

Basically my idea is to find the min rpm and min radius for an artificial gravity via centripetal force wheel based on the percentage of Earth gravity you want within said height of the floor.

r = radius
μ = rpm
g = 9.81
n = distance from floor to keep % within

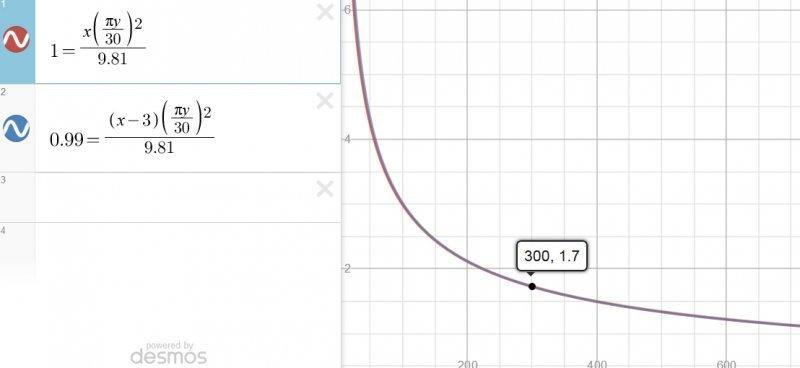
1 = r (π⋅μ /30)² / g

0.99 = (r-n)(π⋅μ /30)² / g

I set some parameters in this graph to keep local g within 3meters of the floor be within 99% of Earth.

My algebra and calc still aren't good enough to do this although I am dying to find out.

I can do this easily with derivative problems using only one variable but I don't want to be cheap and set a proportion for radius to rpm, Without doing that I suspect this might have to be solved with partial derivatives but I don't really know.

I solved it with a graph first, here is what it looks like... Just two lines intersecting,

Is there some general format to solve where two lives intersect?

x = radius
y = rpm

I'm not sure what my next step should be here..
I think I need a decent hint to get going..

I don't know if this is going the right direction although wolfram was able to solve it so maybe its on the right track at least... p = percentage difference from 100% g.

1 - [r (π⋅μ /30)² / g] + [(r-n)(π⋅μ /30)² / g + p] = 1

If you read this far, thank you.

:)

 

[PeroK]

You'd be better off using ω as angular velocity. Then, the centripetal acceleration is given by $ω^2r$.

Unfortunately, you don't need any calculus to solve this!

 

[BiGyElLoWhAt]

This actually would be solved with partials, as you said. Here, check this out: http://tutorial.math.lamar.edu/Classes/CalcIII/RelativeExtrema.aspx

Hopefully you've gotten far enough in your calc studies to understand that. Another thing that I want to point out is that you have unit mismatch going on. You're using RPM (revolutions per minute) you want rPS (radians per second). This will allow you to get the proper values.

On the other hand, you can't really find a minimum for both. You can only find a correct value for one with respect for the other.

 

[julianwitkowski]

Another thing that I want to point out is that you have unit mismatch going on. You're using RPM (revolutions per minute) you want rPS (radians per second).

Thanks, but I'm concerned about the equation now. I originally found the equation on wikipedia about a year ago just looking around, you should check out the page for artificial gravity. Seems like a pretty big mistake for wikipedia to keep because they've kept it up this whole time. I'm certainly no experts so I'd have to leave this up to you guys to change...

Thank you for your advice and the link :)

Unfortunately, you don't need any calculus to solve this!

Well that wouldn't too unfortunate because it's not a calculus course... but I think I see what you mean.

I found μ like this because you can factor out r...

1 - [r (π⋅μ / 30)² / g] + [(r-n)(π⋅μ / 30)² / g + p] = 1 ⇒ 900 g p = π² μ² n

However, I don't see how to factor out mu and keep r instead... Any leads?

 

[PeroK]

You have:

$g = w^2r$
$a = w^2(r-n)$

Where a is the acceleration a distance n from the floor. And that's pretty much all you need.

 

[julianwitkowski]

You have:

$g = w^2r$
$a = w^2(r-n)$

Where a is the acceleration a distance n from the floor. And that's pretty much all you need.

Ok well it sounds like I'm making this much more complicated than it needs to be.
I better read up on this because I've never really used this from what I've learned so far.

Thanks :)

 

[julianwitkowski]

for w = $\frac{|v| sin(θ)}{|r|}$ theta must be in radians as a description of the velocity?

 

[PeroK]

for w = $\frac{|v| sin(θ)}{|r|}$ theta must be in radians as a description of the velocity?

$w = \frac{d\theta}{dt} = \frac{v}{r}$

w is in radians per second.