Calculating net force on four masses around a center mass?

[rockchalk1312]

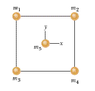
In the figure, a square of edge length 16.0 cm is formed by four spheres of masses m1 = 4.50 g, m2 = 2.80 g, m3 = 0.800 g, and m4 = 4.50 g. In unit-vector notation, what is the net gravitational force from them on a central sphere with mass m5 = 2.10 g?


F = G (m1m2/r²)


To get the radius as a diagonal I used pythagorean's theorem to calculate √16²+16²=11.31m.

I've solved that the force on m1 due to the center particle is (6.67E-11)(4.50 x 2.10/11.31²) = 4.93E-12.

Solving the same way as above:

force on m2: 3.06E-12

force on m3: 8.76E-13

force on m4: 4.93E-12 (same mass as m1)

Was that the right radius to use in the law of universal gravitational equation?

Now that I have those I don't know how to break them into unit vector notation and find the net force? Help please? Figure attached.

 

[haruspex]

Can you write down a unit vector pointing from the central mass to m1?
Btw, you could have made things easier by recognising that each force has a factor m_i, all else being the same. So you could have added up four vectors representing the four masses, then multiplied that by Gm₅/(2d²)

 

[ap123]

To get the radius as a diagonal I used pythagorean's theorem to calculate √16²+16²=11.31m.

You'll need to use 8cm for this calculation instead of 16cm.

I've solved that the force on m1 due to the center particle is (6.67E-11)(4.50 x 2.10/11.312) = 4.93E-12.

Be careful with your units here. To get the force in N, you'll need to use SI units for the other quantities.

 

[rockchalk1312]

Can you write down a unit vector pointing from the central mass to m1?
Btw, you could have made things easier by recognising that each force has a factor m_i, all else being the same. So you could have added up four vectors representing the four masses, then multiplied that by Gm₅/(2d²)

Well what I don't know how to do is break up a diagonally pointing force into i and j components.

And by "has a factor m_i", do you mean that the j component of each force is the same? If so why is that? Would you just add up the four vectors' i components and multiply that by the equation you gave above?

 

[ap123]

Well what I don't know how to do is break up a diagonally pointing force into i and j components.

You just have to find the x- and y-components of the force. These are the i and j components.

And by "has a factor mi", do you mean that the j component of each force is the same? If so why is that? Would you just add up the four vectors' i components and multiply that by the equation you gave above?

haruspex was just trying to save you some effort by noticing that all 4 force equations have a common term Gm₅/r²