Calculating path length difference - help

[Enthusiast94]

Homework Statement

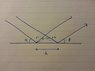
A narrow parallel light beam of wavelength 632.8 nm is incident upon a diffraction
ruler (i.e. the light reflects off of the grating rather than passing through it). The
ruler has 600 lines per mm.

Show that the expression for the condition for constructive interference is
m.lambda = d(cos(alpha) - cos(beta))

Homework Equations

m.lambda=d sin(theta)

The Attempt at a Solution

So the right angle triangle has been formed and path difference (green part) = d.cos(alpha). So, how do I get (- d cos (beta)) in my equation. Also, is the path length I shaded correct?
(Diagram attached)

 

[tiny-tim]

Welcome to PF!

Hi Enthusiast94! Welcome to PF!

So the right angle triangle has been formed and path difference (green part) = d.cos(alpha). So, how do I get (- d cos (beta)) in my equation

isn't there a path difference on both sides?

Also, is the path length I shaded correct?

Yes.

 

[TSny]

Also, is the path length I shaded correct?
(Diagram attached)

It appears that you marked the angle between an incoming ray and an outgoing ray as perpendicular. Is that necessarily so?

 

[Enthusiast94]

Hi Enthusiast94! Welcome to PF!


isn't there a path difference on both sides?


Yes.

It appears that you marked the angle between an incoming ray and an outgoing ray as perpendicular. Is that necessarily so?

Using the new diagram(attached), I've got r1 = dcos(alpha) and r2 = dsin(beta). So now, delta r = r1 - r2 = d(cos alpha - cos beta).

Does this make sense?

 

[TSny]

I would still question whether or not your triangle is a right triangle.

 

[Enthusiast94]

I would still question whether or not your triangle is a right triangle.

Could the given equation be derived w/o considering it as a right triangle? If so, please explain.

 

[tiny-tim]

Could the given equation be derived w/o considering it as a right triangle? If so, please explain.

No, but you need two right-angled triangles …

(the one triangle you've drawn can't be right-angled, can it? )

draw it carefully, and you'll see! ​

 

[TSny]

Could the given equation be derived w/o considering it as a right triangle? If so, please explain.

Try another drawing where the angle in your triangle is not a right angle. Can you still find the path differences by constructing other triangles that are right triangles?

 

[Enthusiast94]

No, but you need two right-angled triangles …

(the one triangle you've drawn can't be right-angled, can it? )

draw it carefully, and you'll see! ​

Try another drawing where the angle in your triangle is not a right angle. Can you still find the path differences by constructing other triangles that are right triangles?

How about this?
But, now the other two angles wouldn't be alpha/beta. :/

 

[tiny-tim]

How about this?

are you deliberately trying to confuse yourself?

the point of a diagram is to help you understand the situation

draw it again, and try to make the right-angles look like right-angles! ​

But, now the other two angles wouldn't be alpha/beta. :/

i'm not sure what you mean

 

[Enthusiast94]

are you deliberately trying to confuse yourself?

the point of a diagram is to help you understand the situation

draw it again, and try to make the right-angles look like right-angles! ​

i'm not sure what you mean

What went wrong in the last diagram? Please be a bit more specific...

As you said, I'll need two right triangles, so I drew a perp from the point at which it strikes to the opposite ray.

 

[tiny-tim]

What went wrong in the last diagram?

those are obviously not right-angles!

you really are kidding yourself if you think that drawings like that will reliably steer you towards the right answers!

 

[Enthusiast94]

those are obviously not right-angles!

you really are kidding yourself if you think that drawings like that will reliably steer you towards the right answers!

It's not about the drawing, it's about sending a message. : )

Anyway, thanks for your help.

 

[TSny]

How about this?

I think you're getting closer. But as tiny-tim mentioned, your dotted lines were not drawn very carefully. Note how the angles that you marked as right angles look quite a bit larger than 90 degrees.

But, now the other two angles wouldn't be alpha/beta. :/

You should be able to use geometry to determine the magnitudes of the angles in your right triangles.