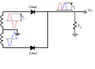
- #1
JJBladester
Gold Member
- 286
- 2
Homework Statement
Calculate the peak voltage across each half of a center-tapped transformer used in a full-wave rectifier that has an average output of 120V.
Homework Equations
Assuming the practical model (factoring voltage drop across diodes but not the diodes' dynamic resistance)...
[tex]V_{out (avg)}=\frac{2(V_{sec}-V_{th})}{\pi }[/tex]
The Attempt at a Solution
[tex]V_{out (avg)}=120V[/tex]
[tex]V_{out (avg)}=\frac{2(V_{sec}-V_{th})}{\pi }[/tex]
[tex]V_{sec}=\frac{(120V)(\pi )}{2}+0.7V=189.196V[/tex]
The voltage across each half of the center-tapped transformer is just half of Vsec:
[tex]\frac{V_{sec}}{2}=\frac{189.196V}{2}=94.598V[/tex]
My book gives an answer of 186V which makes no sense. Given: this book is known to have errata all over the place. Is this another example of a publisher error?