Calculating Percentiles of Standard Normal Distribution

[sami23]

Homework Statement
Normal: mean = 0 standard deviation = 1

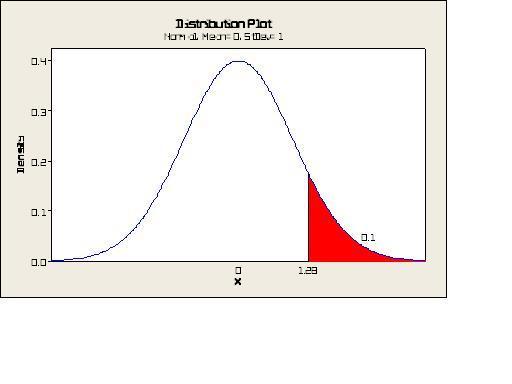
Is it:
10th percentile of standard normal distribution is -1.28
10th upper percentile of standard normal distribution is 0.1
90th percentile of standard normal distribution is -1.28
10th percentile of standard normal distribution is 1.28

The attempt at a solution

Area under the curve is the Population, at the center or x is the mean, let $$\alpha$$/2 be the area shaded in red.


...lost. I know that in standard normal distribution N(mean, variance) = N(0,1) and to get the confidence interval = 1 - $$\alpha$$ = 0.1 which would be 90% (to the left)

I think it would be 10th upper percentile (to the right)

 

[lippyka]

would be 0.1, 10th percentile of standard normal distribution is -1.28 and 90th percentile of standard normal distribution is 1.28? But I am not sure. Could someone please explain this to me? Thank you!